Forum de Mathématiques: Maths-Forum

pas le temps de tester, mais j'ai juste une suggestion : la formule de Leibniz ! :-) S'il y en a qui peuvent essayer, dites si ça fonctionne !

Bonsoir,

Qu'entends-tu par "simplifier" une matrice ?? Ne veux-tu pas dire "réduire" la matrice ?

Oui certes, mais mon problème vient du "trafic" d'indice et du "j-1" dont j'ignore l'origine ben, de manière grossière ... quand i=1, la seconde somme commence à 2, quand i=2, la seconde somme commence à 3 etc ... donc j ayant toujours 1 de plus, alors de j= 1 à i, on a donc 1 d...

Ne vous inquiétez pas ! Je vais continuer à poster et aider sur ce forum ! Il m'a rendu de vrais services durant les deux années de classe prépa, et je veux à mon tour faire mon possible... Mais là, j'avoue que la discussion a tourné au "très très très ridicule" ... Que l'on ne comprenne pas les mat...

Mdr!! après tu dis que tu ne t'énerve pas! Ben désolé, mais là y a de quoi... bon aller, retourne faire des maths, parce que tu as sérieusement besoin d'entrainement. Et arrête de faire dévier le post. On n'est pas ici pour se crêper le chignon, mais pour faire des maths ( niveau Supérieur normalem...

corolle a écrit:marci "petiboulard" mais je n'ai pas besoin de tes réponses! je ne souhaite pas être aidé par quelqu'un qui s'énerve au revoir

Mais je ne m'énerve pas ! ... Non mais franchement, on croit halluciner là ... Aller, je quitte le post ! Bon courage aux suivants !

pour le W, c'est juste le théorème de dérivation te disant que toute fonction constante a pour dérivée la fonction nulle ... Donc là, puisque tu as W(x)= 2 ( qui est donc constante ) , eh bien W'(x) = 0 d'après le cours ... J'ai utilisé toutes mes cartouches ! Je dois y aller ! B...

Ah mais je ne m'énerve pas ! Mais, ce qui est surprenant, c'est que ce genre de questions devrait se trouver plus dans la rubrique "Lycée" que "Supérieur" ... Après, on peut comprendre que tu n'y arrives pas tout de suite, mais essaie au moins d'appliquer nos conseils !!

tu n'as pas encore tout bien lu. Ca n'est pas de la forme uv, c'est de la forme uv+w (le 2 n'est pas multiplié par x). donc u=x ; v=e^-3x ; w=2 u'=1 ; v'=-3e^-3x ; w'=0 et le résultat : u'v+v'u+w' Tu devrais arriver par finir à appliquer correctement les formules. Ahah ... Ericovitchi ... tu viens ...

corolle a écrit:c'est juste?

Toujours pas ...... tu t'obstines à vouloir dériver l'exposant de l'exponentielle ... et tu n'as pas dérivé la fonction constante x ----> 2 ... qui est nulle quand on la dérive ...

Et ce, après touuuuutes nos explications...

Je crois que nous ne pouvons plus rien si tu n'as pas compris ces dernières explications ...

Je te laisse regarder ma dérivation, et la factoriser ...

Oui f(x)=xe^-3x+2 est de la forme U+V = U'V+UV' U=xe^-3x et V =2 U' =1*-3e^(-3*1) =-3e^-3 V' =0 f'(x)= -3e^-3*2 + xe^-3x*0 Non ! Encore loupé ... tu ne poses pas les bonnes fonctions de départ ! Posons U(x) = x V(x) = e^{-3.x} W(x) = 2 on a donc f(x) = U(x).V...

de fait, je n'ai pas lu le post dès le début, mais la fonction que je traitais n'était pas la bonne ! Bref, j'espère que Corolle aura compris au moins ça... Maintenant, en rajoutant le facteur x devant l'exponentielle, ça risque de corser un peu l'explication ;-) Enfin, Corolle, il te suffit de conn...

c'est bon maintenant j'ai -3! alors f(x) = e^-3x donc f'(x)= -3e^-3? j'enlève le x? mais la dérivée de x est 1? donc en fait si on détail, c'est :f'(x)=3*e^-3*1? Non !! comme l'a dit Djmaxgamer tu dérives l'exposant de l'exponentielle, puis tu le laisses tranquille ( oula, j'avoue que mon conseil n...

corolle a écrit:Oui exact, j'ai fais une erreur d'énoncé, il s'agit bien de f(x) =xe^-3x+2
donc f'(x) = 1*3*e^-3+0
en fait la dérivée de e^-3x =3*e^-3?

Non, la dérivée de est ... La constante est

De plus, même si c'est vrai, c'est trompeur : (e^{u(x)})' = u'(x)e^{u(x)} Par exemple : (e^{3x})'=3e^{3x} : (e^{3x})' n'es PAS égal à e^{3x} Exactement, en fait quand tu as f(x) = e^{x} qui donne donc f'(x)= e^{x} ,...

euuuh oui, mais là ce n'est pas pareil !

Dans ton cas, ce n'est pas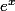 que tu as, mais 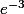qui est une constante. Or quelle est la dérivée d'une constante d'après ton cours ?

Et dans ton exercice, si tu as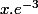 alors en dérivant tu obtiens ?

corolle a écrit:ok, merci black jack!
Pour le calcul de f'(x) j'obtien :

f(x) = xe^-3+2
f'(x) = 1*e^-3 +0

je ne suis pas sûre de la dérivée de e^-3

eh bien dans ton cours, tu as f(x) = x.k ---> f'(x) = k non ? Donc voilà ...

ah ben oui ... vu comme cela ! EFFECTIVEMENT ! Merci beaucoup ! :-D

Bonsoir à tous ! J'espère que vous allez bien, en particulier ceux qui comme moi sont en pleines révisions de concours ! Voilà : j'ai une petite question relative au sujet HEC MATHS III 2007 ( ou peut être bien 2006 ... lol je ne sais plus bref, ... ) On a un endomorphisme "t". On nous fai...