27 résultats trouvés
Revenir à la recherche avancée
Oui, mais je n'ai même pas pensé à regarder
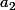
en fait.
J'ai calculé
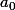
= 1,

= 0, et
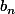
= 0
Donc j'ai dû faire une faute pour

= 0 ?
- par Bitman
- 08 Jan 2011, 16:19
-
- Forum: ✯✎ Supérieur
- Sujet: Identité de Parseval
- Réponses: 5
- Vues: 1148
D'accord, en fait je me suis fait piéger bêtement :ptdr:
Mais je pensais que même en se faisant piéger et en faisant des calculs inutils, on pouvait retrouver
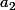
- par Bitman
- 08 Jan 2011, 16:07
-
- Forum: ✯✎ Supérieur
- Sujet: Identité de Parseval
- Réponses: 5
- Vues: 1148
Salut à tous, J'ai un petit problème sur un petit exo, le voici : A l'aide de l'identité de Parseval, montrer que : \bigint_{-\pi}^{\pi} cos^4(x)dx = (3/4)x Pas de problème pour a_{0} = 1 cos²(x) étant paire, b_{n} = 0 Je trouve ensuite a_{n} = 0 Maintenant, voilà comment fait la cor...
- par Bitman
- 08 Jan 2011, 15:55
-
- Forum: ✯✎ Supérieur
- Sujet: Identité de Parseval
- Réponses: 5
- Vues: 1148
Salut, Je bloque sur un petit exo, enfin pas vraiment, j'ai réussi l'exo, mais ne comprends pas vraiment la correction... Voilà l'exo : Soient ;) = {(x,y) R² : x² + y² < 1} et F(x,y) = (y² , x) Vérifier le théorème de Green. Alors pour le calcul de \bigint_{\partial \Omega} F . dl , il font : \big...
- par Bitman
- 18 Nov 2010, 21:41
-
- Forum: ✯✎ Supérieur
- Sujet: Petite question sur les intégrales
- Réponses: 6
- Vues: 587
Alors f(x) = -1/4x²+2x
Tu sais dériver -1/x² et x
Alors il suffit de réécrire f(x) de manière à ce que tu voies comment le dériver.
Par exemple, f(x) = (1/4)(-1/x²) + 2x
Et tu devrais voir comment dériver cela assez facilement.
- par Bitman
- 16 Nov 2010, 21:06
-
- Forum: ✎✎ Lycée
- Sujet: Aide Derivé
- Réponses: 3
- Vues: 466
Oui mais alors comment ferais tu pour d/dx(dg/dr), dg / dr étant une fonction où les variables sont r et ;) En fait j'aime bien voir g comme g(r(x,y),;)(x,y)), ainsi on peut selon moi dire que g dépend de x et de y Et je comprends mieux l'égalité sous cette forme : dg/dx = (dg / dr)(dr / dx) + (dg /...
- par Bitman
- 15 Nov 2010, 13:33
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
Merci j'ai essayé de chercher une démonstration mais n'en ai pas trouver... Tempis, je bloque de toute façon toujours plus loin dans l'exercice... g(r,;))=f(x(r,;)),y(r,;))) J'ai df/dx = (dg / dr)(dr / dx) + (dg / d;))(d;) / dx) = (dg / dr)(x / r) - (dg / d;))(y / r²) Et ensuite pour d²f/dx² = (d(dg...
- par Bitman
- 15 Nov 2010, 10:36
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
C'est encore moi.... Je suis désolé mais c'est encore pour le même type d'exercice, mais en coordonnée polaire. http://dl.dropbox.com/u/14698843/gradient2.jpg En gros je déduis que f(x,y) = g( r(x,y) , ;)(x,y) ) Dans la correction, il font ainsi : df/dx = (dg / dr)(dr / dx) + (dg / d;))(d;) / dx) Je...
- par Bitman
- 15 Nov 2010, 00:12
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
Merci de ces explication :) Mais mon prof nous a peut-être mal expliqué quelque chose ( ou j'ai très probablement mal compris ) Mais en gros si j'ai df/dx ( pour le gradient par exemple ), pour avancer je fais : df /dx = ( df / dr )( dr / dx ) Mais ducoup, lorsque j'ai d²f / dx², je dis : d²f/dx² = ...
- par Bitman
- 14 Nov 2010, 01:09
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
Ah ok :D Sinon j'ai une petite question encore; Pour la question 2 tout a l'heure, ma faute était que lorsque j'avais genre dr/dx², je dérivais 2 fois r en x... Je me suis rendu compte de l'erreur en voulant le recopier sur le forum... Mais que représente cette quantité ? Enfin y a-t-il un moyen de ...
- par Bitman
- 14 Nov 2010, 00:42
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
Merci beaucoup Ben314 et Nightmare !
J'ai tout compris :)
Je voulais vous montrer ce que j'avais fais pour la 2, mais en le recopiant, j'ai trouvé mon erreur. Merci beaucoup :)
D'ailleurs j'en profite pour vous demander, que représentent les quantités dr / dx² ou encore d²f/dr
- par Bitman
- 13 Nov 2010, 23:16
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038
Oui, je voulais dire r ( pas en gras ) est fonction de x,y et z. ( Enfin tu as l'air de dire le contraire ^^ ) Je vois pas exactement ce que tu me demandes concernant le gradient d'une fonction, c'est pour moi un vecteur dont chaque composante représente la dérivé de cette fonction en une de ses var...
- par Bitman
- 13 Nov 2010, 21:55
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice "facile" sur Laplacien
- Réponses: 32
- Vues: 2038