Forum de Mathématiques: Maths-Forum

ah ok T(n)=(n-1)! ?

I(n,n) n'est ce pas plutot (n+1)!²/(2n+2)! ?

Oh oui! merci beaucoup, ça me plait bien tout ça!

d'accord, merci

aucune idée?

Pour ce qui est de l'integrale, je trouve :
que je n'arrive pas à simplifier..
Donc ca n'aide pas trop non plus..

oui c'est bien comme ça que je pensais.. Donc ca ne me sert à rien non plus pour le sens d'orientation d'etudier la limite de ...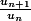
En ce cas je ne vois pas trop comment simplifier..

Qu'est ce que tu veux me faire dire sur 1+1/n et 1-1/n?

je ne sais pas d'où sort l'exercice..
non je n'ai pas calculé l'integrale

puis j'ai du mal à comprendre le fait que si qqchose est equivalent à autre chose en l'infini ils aient même variation

aoups j'avais oublié un truc, j'ai mal recopié..

Deja essayé.. mais c'est pas simple

Voilà, j'essaie pas mal de choses mais je m'embrouille, j'arrive à rien..
Auriez vous une suggestion pour montrer que la suite:
u(n):=
est croissante?

d'ac merci, j'ai pu voire ce dont il s'agit!

comment résoud t-on:
y'=2xy/(x²-y²)
je pensais metre sous la forme d'une somme de dérrivées partielle:
(x²-y²)dy-2xydx=0
mais ne vérifie pas schwartz..

pensez vous que ce soit possible?

J'aimerais pouvoir borner au plus près les dérivés successives de x^{n}(1-x)^n,pour x entre 0 et 1 je ne trouve rien de bien concluant..
Meme probleme pour exp((x-1)^2n/x²)
Quelqu'un aurait il une idée, une piste?

oui mais le cosinus hyperblique et le sinus hyperbolique sont des "formes déguisées d'exponentielle", en fait les seule fonction à divergence rapide sont les exponentielles et les fonctions construites à partir d'exponentielles?

peux tu m'en donner un exemple?

une telle fonction est elle forcement de cette "forme"?(l'integrale de l'exponentielle d'inverse)?