Forum de Mathématiques: Maths-Forum

Oui je vois :)
Merci !

Merci pour cette explication, je crois que je comprends.
Alors le N dépend ensuite uniquement de epsilon (p dépendant lui-même indirectement de epsilon)..

Euh..

avec n'importe quel p supérieur à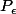 (il en existe autant qu'on veut car 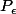existe pour toute valeur de epsilon).
?

Merci à tous pour votre aide et vos réponses détaillées. Juste une petite confirmation : la question suivante demande de montrer que C_0 , le sous-espace vectoriel de l_\infty des suites qui convergent vers 0, est fermé dans l_\infty . Si j'ai bien compris, je peux appliquer la même méthode: Je pren...

@Ben314 : je vois, effectivement un majorant qui dépend de n ne peut être utilisé pour montrer que la suite est bornée. Dans ce cas, est-ce possible d'utiliser la définition de la convergence uniforme de (c_p)_{p\in \mathbb{N}} pour obtenir un \epsilon qui ne dépend pas de n et donc un major...

@Ben314, arnaud32 : Vous avez étés plus rapides. Je comprends ce que vous voulez dire pour l'impossibilité de démontrer le fait que s_n est bornée en la majorant par un terme qui dépend de n. Si je comprends bien, il faut : 1) déduire du "sup" le fait que l'expression dans le sup est vraie...

Ahh, attendez, je pense que j'ai compris. Dans la définition de la suite de Cauchy, j'ai sup\{|c_p(n)-c_q(n)|, n\in \mathbb{N}\} < \epsilon . À l'intérieur de ce sup, je fais tendre q vers l'infini (j'ai le droit car je sais que c_q(n) tend vers s_n , la convergence ponctuell...

Bonjour, Merci pour votre réponse. La majoration de |s_n| est maintenant OK : \forall p\in \mathbb{N}, |s_n|=|s_n - c_p(n) + c_p(n)| \leq |c_p(n)| + |c_p(n)-s_n| Il est facile de majorer le terme de droite car la suite c_p est bornée par définition (de valeur absolue ...

Bonjour, Je cherche à montrer que l'espace métrique des suites bornées muni de la distance de la convergence uniforme est complet. Je bloque sur la question suivante : comment puis-je démontrer qu'une suite de suites (réelles), qui converge, simplement vers une suite converge également uniformément ...

Merci beaucoup, c'est plus concis comme ça :)

Bonjour,

Je n'arrive pas à prouver une inégalité simple à deux variables avec des infs.
Comment faire pour éviter de considérer tous les cas ?

Voici :



avec u, v des nombres réels positifs.

Merci d'avance pour vos suggestions !

Il s'agit de l'ensemble des suites réelles bornées, munies d'une distance qui ne fait pas dans la dentelle.

Pardon, je me suis mal exprimé. Imaginons que je dispose d'un espace métrique particulier dont la distance est définie (et connue). Je dois montrer qu'il est complet (l'enseignant qui a composé l'exercice sait que son espace métrique est complet, mais moi je ne l'ai pas encore démontré). Comment pui...

Bonjour, Quelle est la méthode "standard" pour montrer qu'un espace métrique est complet ? J'ai un espace métrique dont la distance est explicitée. Je suis bloqué dans les deux cas suivants : -Je prends une suite de Cauchy quelconque, et j'essaie de montrer qu'elle est convergente. Mais co...

Merci pour votre réponse, je suis rassuré :)

Bonjour, Je suis face à un exercice qui demande de montrer que tout polynôme à coefficients complexes se prolonge de façon unique en une fonction continue de la sphère de Riemann dans elle-même. En excluant les polynômes de degré \leq 1 pour lesquels le prolongement est la fonction définie par le mê...

Bonjour Ben, Merci beaucoup pour cette réponse détaillée. J'aime bien l'explication de tout voisinage de l'infini (ou de zéro) qui intersecte C*.. Effectivement, la définition que j'ai dans mon livre semble passer sous silence le fait que ce n'est qu'une condition nécessaire pour avoir un prolongeme...

Bonjour, Je suis confronté à un exercice demandant de montrer qu'une fonction de \mathbb{C}^{*} dans lui-même (en l'occurence celle qui associe z à z^n ) se prolonge de façon unique en une fonction continue de la sphère de Riemann dans elle-même. Or la définition dont je dispose du prolongement d'un...

Bonjour, Pour une application f: X\rightarrow Y : Que signifie f^{-1}(\zeta) quand \zeta est un ensemble de parties de Y (c'est à dire \zeta \subset P(Y) ) ? Je connais cette notation dans le cas particulier où \zeta est une tribu (tribu image réciproque), mais que signifie cette not...

Merci beaucoup à vous deux pour ces précisions, c'est effectivement la "clé" qui me manquait. Mon livre d'intégration (Pagès) démontrait bien sûr que l'union dénombrables d'ensembles dénombrables est dénombrable, mais je n'avais pas vu (et de fait, j'ai l'impression qu'elle n'y figure pas) la propos...