11 résultats trouvés
Revenir à la recherche avancée
Et quel est le problème? Si tu veux "trouver" la réponse formallement, considére la suite 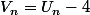 .
. 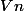 vérifie
vérifie ^n=-\frac{3}{4}V_n$) , donc évidement
, donc évidement 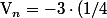^n $) et
et 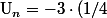^n + 4 $)
- 24 Avr 2006, 22:45
- Forum: ✎✎ Lycée
- Sujet: probleme sur les suites
- Réponses: 4
- Vues: 527
Voilà une solution courte: Par MA-MG on a $(\frac{x}{y}+\frac{x}{y}+\frac{y}{z})/3 \geq (\frac{x^2}{yz})^{1/3} = \frac{x}{(xyz)^{1/3}} \geq x$ . De manière analogique on a $(\frac{z}{x}+\frac{y}{z}+\frac{y}{z})/3 \geq y$ et $(\frac{z}{x}+\frac{z}{x}+\frac{x}{y}...
- 24 Avr 2006, 22:30
- Forum: ⚔ Défis et énigmes
- Sujet: inegalité tres joli !!! ;)
- Réponses: 9
- Vues: 1588
Ok, on peut faire comme ça. Si  et vérifier que le minimum est plus grand que 0. Le calcul pour ça est bien direct mais un peut dificile pour écrire donc je n'écris le pas ici.
et vérifier que le minimum est plus grand que 0. Le calcul pour ça est bien direct mais un peut dificile pour écrire donc je n'écris le pas ici.
- 09 Avr 2006, 15:19
- Forum: ⚔ Défis et énigmes
- Sujet: inegalité tres joli !!! ;)
- Réponses: 9
- Vues: 1588
Alors, on peut utiliser l'inégalité de Holder avec $p=1+\varepsilon$ pour $\varepsilon>0$ arbitrairement petit. Dans ce cas $q=\frac{1}{\varepsilon}+1$ . On obtient $\frac{x}{y}+\frac{y}{z}+\frac{z}{x} \geq (x^p+y^p+z^p)^2 (\frac{1}{x^q}+\frac{1}{y^q}+\frac{1}{z^q})^{1/q}$ (attention...
- 09 Avr 2006, 14:20
- Forum: ⚔ Défis et énigmes
- Sujet: inegalité tres joli !!! ;)
- Réponses: 9
- Vues: 1588
- 09 Avr 2006, 13:40
- Forum: ⚔ Défis et énigmes
- Sujet: inegalité tres joli !!! ;)
- Réponses: 9
- Vues: 1588
Donne cours particuliers en maths à Paris
Bonjour,
Je suis un étudiant de troisième année à l'Ecole Normale Supérieure à Paris. Maintenant je cherche à donner des cours en maths. Si vous êtes interessés, math_cours_particuliers@yahoo.fr ou 0617531326.
Je suis un étudiant de troisième année à l'Ecole Normale Supérieure à Paris. Maintenant je cherche à donner des cours en maths. Si vous êtes interessés, math_cours_particuliers@yahoo.fr ou 0617531326.
- 08 Avr 2006, 22:07
- Forum: ⚖ Place de marché
- Sujet: Donne cours particuliers en maths à Paris
- Réponses: 0
- Vues: 1651
On peut utiliser le théorème de Pascal. Soit F le point d'intersection de la ligne de B parallelle à DE et de la ligne de C parallelle à AE. Considérons le hexagone AEDCFB (attention à l'ordre des sommets, c'est très important!). Tous les côtes opposées dans ce hexagone sont parallelles, c-a-d que t...
- 08 Avr 2006, 21:21
- Forum: ⚔ Défis et énigmes
- Sujet: difficile
- Réponses: 2
- Vues: 1242
Tu toujours arrive au terme suivant en passant tous les carreaux du carré à droite et à l'haut de dimension paire (i.e. pour 5 c'est le carré 1-2-3-4, pour 17 le carré avec les sommets 7, 10, 13 et 16 etc.), c'est bien évident du dessin. Donc tu a raison, la formule est 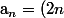^2+1$)
- 08 Avr 2006, 20:43
- Forum: ✎✎ Lycée
- Sujet: Dm de maths un peu complexe
- Réponses: 2
- Vues: 1057
Comme  , on a
, on a  . En particulier,
. En particulier,  ,
,  et
et  . En prenant la somme des ces trois dernières inégalités et en divisant le resultat par
. En prenant la somme des ces trois dernières inégalités et en divisant le resultat par  on conclut.
on conclut.
- 08 Avr 2006, 20:15
- Forum: ⚔ Défis et énigmes
- Sujet: inegalité tres joli !!! ;)
- Réponses: 9
- Vues: 1588
- 11 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
