bonsoir,
pas besoin de factoriser :
quelle est la limite de e(x) en - l'infini?
18 résultats trouvés
Revenir à la recherche avancée
- 08 Déc 2008, 22:30
- Forum: ✎✎ Lycée
- Sujet: Exercice exponentielle
- Réponses: 9
- Vues: 852
Non, en fait je me suis simplifier maladroitement le problème
D'où l'oublie de cas possible et donc du résultat nécessairement faux
D'où l'oublie de cas possible et donc du résultat nécessairement faux
- 11 Nov 2008, 00:03
- Forum: ⚔ Défis et énigmes
- Sujet: J'ai perdu la boule .
- Réponses: 14
- Vues: 1467
Hello
Je suis arrivé à 1/37 mais un peu trop rapidement,
Vraiment trop rapidement ou suis-je arrivé par chance à la bonne réponse?
Je suis arrivé à 1/37 mais un peu trop rapidement,
Vraiment trop rapidement ou suis-je arrivé par chance à la bonne réponse?
- 10 Nov 2008, 23:55
- Forum: ⚔ Défis et énigmes
- Sujet: J'ai perdu la boule .
- Réponses: 14
- Vues: 1467
Bonsoir,
Sinon, il faut prendre en compte les racines du polynome, une t'etant donnée
Tu peux alors factoriser par) où
où  est la racine donnée
est la racine donnée
Sinon, il faut prendre en compte les racines du polynome, une t'etant donnée
Tu peux alors factoriser par
- 10 Nov 2008, 23:25
- Forum: ✎✎ Lycée
- Sujet: degré de polynôme
- Réponses: 4
- Vues: 648
magnum13 a écrit:y² + y -20 =0
[y = -5 ou y = 4]
Ce serait pas un polynome du 2° degrée?
PS: Ca correspond pas peut etre pas à ce attendu?
- 10 Nov 2008, 23:08
- Forum: ✎✎ Lycée
- Sujet: Polynôme du second degré
- Réponses: 14
- Vues: 2458
Merci, j'ai relu mon cours dans un doute qui me saoulait un peu trop,
je faisais au début la meme erreur par décalage de la courbe
Ah je suis mauvais :ptdr:
je faisais au début la meme erreur par décalage de la courbe
Ah je suis mauvais :ptdr:
- 10 Nov 2008, 22:52
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
- 10 Nov 2008, 22:42
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
- 10 Nov 2008, 22:36
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
- 10 Nov 2008, 22:29
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
- 10 Nov 2008, 22:27
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
Je me suis armé d'un crayon est en effet,
C'était trop facil, :hum: , c'était pourtant une idée originale
Je pensais à ça quand je pensais à plusieurs solutions :triste:
Faut reprendre
C'était trop facil, :hum: , c'était pourtant une idée originale
Je pensais à ça quand je pensais à plusieurs solutions :triste:
Faut reprendre
- 10 Nov 2008, 22:21
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
- 10 Nov 2008, 22:12
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
Le raisonnement est juste,
Pas d'erreur de calcul,
Donc, oui la réponse est juste
(pour te convaincre verifie les valeurs dans ton systeme de départ)
:++:
Pas d'erreur de calcul,
Donc, oui la réponse est juste
(pour te convaincre verifie les valeurs dans ton systeme de départ)
:++:
- 10 Nov 2008, 22:11
- Forum: ✎✎ Lycée
- Sujet: Polynôme du second degré
- Réponses: 14
- Vues: 2458
Désolé, je me suis embrouillé,
Quoi qu'il en soit, il n'y aurait pas un second théorème où l'on dit :
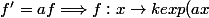) ?
?
Quoi qu'il en soit, il n'y aurait pas un second théorème où l'on dit :
- 10 Nov 2008, 21:59
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
Il manque pas une donnée dans l'énoncé,
Je trouve plusieurs solutions,
Je l'ai pas ecrit mais graphiquement, je m'imagine plein de courbes differentes
:doh:
Je trouve plusieurs solutions,
Je l'ai pas ecrit mais graphiquement, je m'imagine plein de courbes differentes
:doh:
- 10 Nov 2008, 21:49
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
D'après ton schéma: M est l'intersection des droites (BC) et (GH) (car elle appartiennent au meme plan (GHE) ) On construit D tel que D intersection de (AM) et (FH) (car sur le plan (FGH) ) On obtient le quadrilatere ABCD qui appartient à (ABC) avec A,B,C,D des points qqconque de [FG], [EG], [EH] et...
- 10 Nov 2008, 21:44
- Forum: ✎✎ Lycée
- Sujet: Section d'un tétraèdre par un plan
- Réponses: 6
- Vues: 2767
- 10 Nov 2008, 21:28
- Forum: ✎✎ Lycée
- Sujet: Problème Tle S
- Réponses: 45
- Vues: 2429
Salut,
Il s'agit de déterminer la section sur le dessin?
Et, B appartient à (EG) où au segment [EG]?
En attente de plus d'info
Il s'agit de déterminer la section sur le dessin?
Et, B appartient à (EG) où au segment [EG]?
En attente de plus d'info
- 10 Nov 2008, 21:22
- Forum: ✎✎ Lycée
- Sujet: Section d'un tétraèdre par un plan
- Réponses: 6
- Vues: 2767
- 18 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
