Forum de Mathématiques: Maths-Forum

Merci bien, c'est exactement ce qu'il me fallait pour finir !

Bonne soirée !

Bonsoir, Je m'amusais juste à calculer une intégrale de 3 manières différentes, mais je n'ai pas réussis à conclure avec une des 3 méthodes (les 3 méthodes m'ont été proposé par mon professeur donc devraient toutes 3 aboutir sans problèmes). Voici donc l'intégrale: \Bigint_{0}^{a} sqrt(b^2+x^2&#...

Exact pour le 1 qui devrait être un -1, mais cela ne change strictement rien à la méthode, ce sera maintenant: - u(e_{i}) \in Vect(e_{i}) donc la conclusion reste la même. Pour la fin c'est juste que je n'ai pas redétaillé: Je prouve que tout les k_{i} sont égaux en reconsidérant d'a...

Considérons la symétrie orthogonale s par rapport à l'hyperplan de vecteur normal le vecteur canonique de base e_{i} avec i compris entre 1 et n : On a: E_{s}(-1)=Vect(e_{i}) u(s(e_{i}))=u(-e_{i}) u(s(e_{i}))=s(u(e_{i})) d'ou : ...

Très bonne idée, merci beaucoup j'ai pu finir l'exercice ainsi :happy2:

(Je ne sais pas si je suis censé expliciter le détail de la méthode pour d'autres usagers du forum ? Si oui merci de me faire signe et je résumerais ma démarche !)

Bonne soirée !

Bonsoir, Je bloque sur un petit exercice d'algèbre linéaire... Soit E un espace-vectoriel de dimension n finie, u un endomorphisme de E. Montrer que si u commute avec toute isométrie vectorielle alors u est une homothétie. Si quelqu'un à des pistes pour la dimension n quelconque... je bloque un peu ...

Ya des jours ou je me sens bête :ptdr:

Merci beaucoup !

Bonne soirée !

Aie aie aie, en effet^^ C'était déja plus facile... Merci :ptdr: Je comptais en fait me servir de ça pour montrer la convergence de: \int_0^{\infty} sin(t)sin(1/t)dt Et je tourne toujours en rond, mais déja un peu moins loin ! (Je voulais utiliser le critere d'équivalence, mais comme...

Bonjour bonjour,

Je cherche à montrer la convergence de:


(J'ai déja montré la convergence de:



Mais je ne sais pas si ça peut servir...)

Des idées ?

Parfait, j'ai utilisé


ce qui me donne comme primitive:


Merci beaucoup :we:

Bonne soirée !

Bonjour,

Je cherche à retrouver la méthode qui permet de me donner une primitive de:


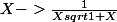
Merci d'avance !

A vrai dire je viens de lire ça sur un corrigé, qui cite juste Cauchy-Lipschitz pour affirmer ça. Mais effectivement je n'ai pas réussi à montrer que l'équation vérifie les conditions d'application du théorème... f(t) est simplement continue, et non C1.

Quelqu'un pour apporter plus de précisions ?

L'autre inégalité est évidente, pardon je m'en vais me cacher :zen:

Bonne soirée !

Effectivement, pour l'application du théorème de rang à gof j'ai du m'endormir :dodo: Bon ok ma stupidité corrigé, j'ai la moitié de la preuve de faite: Th. du rang à gof: rg(gof) - dim(E) = -dim(Ker(gof)) Or: dim(Ker(gof)) >= dim(Ker(f)) (car Ker(f) inclus dans Ker(gof)) d'ou: rg(gof) - dim(E) <= -...

(J'aurais peut-être du préciser que je suis en spé étoile.) Je me doute que la démonstration doit être simple, d'autant plus que le résultat paraît évident... mais j'ai pas encore réussis à formuler ça correctement... :triste: gof(E) contenu G nous indique que rg(gof) <= dimG, mais ce n'est d'ailleu...

Le rang de l'application linéaire canoniquement associé par exemple, cad la dimension de son image...
On peut biensur raisonner en termes d'endomorphismes si c'est plus simple.

Bonsoir,

Je cherche à démontrer le résultat suivant:


avec A matrice n*p et B matrice p*m (donc AB matrice n*m).

Quelqu'un à t-il des idées de démonstration à proposer ?

Merci d'avance !

Merci bien, j'ai résolu le problème :++:

Pour information, il était également possible de répondre à l'aide du théorème Cauchy-Lipschitz:
Si y(t1)=y'(t1)=0 on montre que y est identiquement nulle !

Merci bien Purrace, mais le wronskien ne fesant pas (encore ?) parti de mon bagage, je ne l'ai jamais utilisé et j'ai quelques mal à le faire ici. Pour information, je me suis documenté sur wikipedia: Wronskien sur wikipedia Je pense à une solution particulière du type: y1(t)=sin(sqrt(m)*(t-t1)), ai...

Bonsoir,

y''(t3) n'implique pas y(t3)=0 car on peut avoir f(t3)=0, on sait seulement de f qu'elle est continue.

Aux erreurs de raisonnement près,

D'autres idées ? Ou rectificatif ?