ah oki ! c'est une factorisation.
Bref je te remercie, j'vais regarder tout ça !
376 résultats trouvés
Revenir à la recherche avancée
- 19 Juin 2010, 11:17
- Forum: ✯✎ Supérieur
- Sujet: Equation cubique
- Réponses: 5
- Vues: 726
- 19 Juin 2010, 11:05
- Forum: ✯✎ Supérieur
- Sujet: Equation cubique
- Réponses: 5
- Vues: 726
Equation cubique
Bonjour tout le monde ! Je bloque sur un exercice et je ne sais pas comment commencer, si vous pouviez me filer un petit coup de main ce serait sympa : Montrer que pour tout p premier, l'équation 3x^3+4y^3+5z^3=0[p] possède une solution non nulle sur \mathbb{F}_p^3 . J'ai essayé de faire comme pour ...
- 18 Juin 2010, 23:05
- Forum: ✯✎ Supérieur
- Sujet: Equation cubique
- Réponses: 5
- Vues: 726
La forme générale d'une solution de ton équation est :
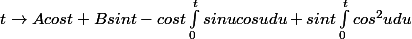
(sauf erreur de calcul)
On peut simplifier le résultat vu que les intégrales se calculent bien.
Avec une variation de la constante tu peux trouver ça.
(sauf erreur de calcul)
On peut simplifier le résultat vu que les intégrales se calculent bien.
Avec une variation de la constante tu peux trouver ça.
- 05 Avr 2010, 14:45
- Forum: ✯✎ Supérieur
- Sujet: équation différentielle de second ordre
- Réponses: 8
- Vues: 1086
Un petit résultat à ce propos, \int_{0}^{1} x^xdx=\bigsum_{n=1}^{+oo} \frac{(-1)^n}{n!} ça te servira surement pas mais c'est joli :we: je sais pas d'où tu tiens ce résultat mais la somme de droite se calcule : \bigsum_{n=1}^{+\infty} \frac{(-1)^n}{n!}=sh(1)-1-ch(1)=...
- 08 Jan 2010, 21:25
- Forum: ✯✎ Supérieur
- Sujet: Intégrale x^x
- Réponses: 10
- Vues: 764
ah oui merci 
j'ai été maladroit, je parlais des Ker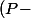(u)) )
)
comme je n'avais pas que Q=ppcm(minimaux des ei) on décomposait d'abord E par lemme des noyaux.
Merci encore !
j'ai été maladroit, je parlais des Ker
comme je n'avais pas que Q=ppcm(minimaux des ei) on décomposait d'abord E par lemme des noyaux.
Merci encore !
- 19 Déc 2009, 19:00
- Forum: ✯✎ Supérieur
- Sujet: polynome minimal
- Réponses: 6
- Vues: 604
salut !
merci de vos réponses !
on m'a conseillé d'utiliser les sous espaces caractéristiques ce qui évite de décomposer Q en irréductibles et donne directement les P_r, apres on utilise ce que vous dites pour conclure, ie que x+y possède comme polynome minimal

thanks !
merci de vos réponses !
on m'a conseillé d'utiliser les sous espaces caractéristiques ce qui évite de décomposer Q en irréductibles et donne directement les P_r, apres on utilise ce que vous dites pour conclure, ie que x+y possède comme polynome minimal
thanks !
- 19 Déc 2009, 18:18
- Forum: ✯✎ Supérieur
- Sujet: polynome minimal
- Réponses: 6
- Vues: 604
polynome minimal
bonsoir à tous !! je ne sais pas par où commencer avec cet exercice... Soit E un K-ev de dimension finie et u dans L(E). On note pour x dans E, \prod_{u,x} le polynôme de degré minimal et unitaire de l'idéal { P\in K[X], P(u)(x)=0 }. Montrer qu'il existe x dans E tel que \prod_{u,x}=...
- 13 Déc 2009, 21:15
- Forum: ✯✎ Supérieur
- Sujet: polynome minimal
- Réponses: 6
- Vues: 604
Série entière, radical complexe
Bonjour à tous ! Mon prof m'a donné un article où l'on avait une série entière égale à H(t)=\frac{(1-t+\sqrt(1-6t+t²))}{4} pour la variable t complexe. Il est écrit que le rayon de convergence de la série entière est égale à la plus petite des racines du trinôme dans le radic...
- 20 Oct 2009, 05:05
- Forum: ✯✎ Supérieur
- Sujet: Série entière, radical complexe
- Réponses: 1
- Vues: 950
Nightmare a écrit:Salut !
Fais un développement asymptotique, tout s'arrange !
mais j'ai besoin de majorer la norme infinie, non ?
- 04 Sep 2009, 17:41
- Forum: ✯✎ Supérieur
- Sujet: Convergence uniforme
- Réponses: 3
- Vues: 781
Convergence uniforme
Salut tout le monde ! Ben voilà c'est la reprise et là je bloque sur un exercice de suite de fonctions, j'espère que vous pourrez m'aider pour avancer dans celui-ci =D : On considère les f_n(x)=nsin(\sqrt{ x+4\pi^2n^2}) . Cette suite de fonctions converge vers x\to \frac{x}{4\pi} . M...
- 04 Sep 2009, 16:34
- Forum: ✯✎ Supérieur
- Sujet: Convergence uniforme
- Réponses: 3
- Vues: 781
ouai y a des trucs marrants sur les matrices magiques, il y a par exemple des algorithmes pour remplir les carrés magiques de n'importe quel ordre, pourvu que celui-ci soit impair. Quand c'est pair c'est plus dur... Tu peux aussi créer des produits sur les matrices magiques qui te donnent en sortie ...
- 01 Sep 2009, 20:52
- Forum: ✯✎ Supérieur
- Sujet: matrices magiques
- Réponses: 2
- Vues: 2639
achille a écrit:Salut tous,
J'ai besoin de ça pour la philo (eh oui!) : si deux fonctions définies sur un intervalle sont égales sur une partie dense de celui-là, seraient-elles égales ?
si elles sont continues oui
- 31 Aoû 2009, 11:25
- Forum: ✯✎ Supérieur
- Sujet: égalité ?
- Réponses: 17
- Vues: 1961
Salut,
Hmm rien n'empêche la fabrication d'un ensemble comme ça à mon avis.
C'est une partie de (R² U R^3)
Hmm rien n'empêche la fabrication d'un ensemble comme ça à mon avis.
C'est une partie de (R² U R^3)
- 12 Aoû 2009, 17:58
- Forum: ✯✎ Supérieur
- Sujet: Est-il licite de construire un ensemble dont les éléments n'ont pas le même type ?
- Réponses: 5
- Vues: 1131
- 10 Aoû 2009, 18:16
- Forum: ✯✎ Supérieur
- Sujet: Théorème de la fonction inverse
- Réponses: 4
- Vues: 2976
Salut,
Oui l'absurde c'est le plus simple. Reviens à la définition de la divergence. Prends un A>u_0 par exemple et regarde ce que ça implique.
PS : es-tu sûr de la définition de ta suite parce qu'elle semble étrage :id:
Oui l'absurde c'est le plus simple. Reviens à la définition de la divergence. Prends un A>u_0 par exemple et regarde ce que ça implique.
PS : es-tu sûr de la définition de ta suite parce qu'elle semble étrage :id:
- 06 Aoû 2009, 14:35
- Forum: ✯✎ Supérieur
- Sujet: Suite périodique
- Réponses: 18
- Vues: 4596
quand je disai 1 est solution je pensai au triplet (1,1,1 ) excuse moi pour le manque de rigueur. J'ai déja résolu ce système par pivot de Gauss.c'est la que j'ai obtenu (0,0,0) Un ami m'a dit qu'il fallait faire des opération sur les lignes jusqu'a trouver quelque chose de la forme .a*(mx+my+mz) =...
- 06 Aoû 2009, 13:28
- Forum: ✯✎ Supérieur
- Sujet: Système à paramètre
- Réponses: 7
- Vues: 984
j'obtient sauf erreur de calcul x=y=z=0 Mais il est evident de voir que 1 est solution pour \lambda = 1 hmm ce n'est pas correct de dire que 1 est solution, en fait les solutions sont des triplets (x,y,z). Par exemple (1,1,1) est solution puisque c'est ça que tu dois montrer. Par homogénéité, les (...
- 06 Aoû 2009, 09:20
- Forum: ✯✎ Supérieur
- Sujet: Système à paramètre
- Réponses: 7
- Vues: 984
en fait t'as pas besoin de t'occuper du cas A>0 parce que tu veux aller en  . Si tu veux montrer que ça tend vers
. Si tu veux montrer que ça tend vers  ça veut dire que c'est forcément positif à partir d'un certain rang.
ça veut dire que c'est forcément positif à partir d'un certain rang.
- 05 Aoû 2009, 18:48
- Forum: ✯✎ Supérieur
- Sujet: Suites et limites
- Réponses: 6
- Vues: 747
Je suis coincé et à part résoudre ce système ( facile ) je n'arrive pas à répondre à ce qui est demandé pouvez me donner un coup de pouce :++: ? Soit a \in ]0.1/2[ un réel fixé Pour tout \lambda \in \mathbb{R} on définit le système paramétré par \lambda et d'inconnues ( x,y,z ) \left\{ \begin{array...
- 05 Aoû 2009, 17:01
- Forum: ✯✎ Supérieur
- Sujet: Système à paramètre
- Réponses: 7
- Vues: 984
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
