Forum de Mathématiques: Maths-Forum

Ben en posant 3$\rm u=\sqrt{2xt^{2}+1} ça vient tout seul. Je garde ma simplification, à savoir t=1. Si 3$u=\sqrt{2x+1} , 3$du=\frac{dx}{\sqrt{2x+1}} ie 3$udu=dx . et puis 3$x=\sqrt{\frac{u^2-1}{2}} donc si on intègre entre 1 et x par exemple, 3$C(x)=C(1)+\sqrt{2}\int_{\sqrt{3}} ^{s...

Bonsoir , les concours sont finit , c'est enfin les vacances ! J'ouvre ce topic pour vous demander de nous dire ce que vous avez eu : Pour ma part j'ai eu les mines , toutes les centrales , mais j'ai loupé X et les ens , j'ai donc decidé de cuber . A vous ! waouh moi j'ai eu que l'ENSIMAG et j'hési...

Si on suppose qu'on intègre entre 0 et 1 pour simplifier. Une solution de l'ESSM est x\to\frac{1}{\sqrt x} . Si u(x)=\frac{C(x)}{\sqrt x } , je tombe sur un truc de la forme : C'(x)=\frac{1}{2}\frac{3^{\sqrt{2x+1}}}{\sqrt x } et je t'avoue que j'ai du mal à intégrer ça ^^'.

bonsoir, déjà merci à tous pour l'importance que vous accordez cette fois à mon sujet :-) pour commencer: * la justification de la dérivée avec le signe intégrale est, effectivement comme disait un de nos amis, pas nécessaire puisqu'il s'agit de primitive I.e dans le domaine convenable. * pour ce q...

skilveg a écrit:Qu'est-ce que tu dis de la série ?

je dis merci ! j'y avais pas pensé :id:

non justement, j'essaie de trouver un contre exemple mais sans succès, c'est pour ça que je demande ^^'. En fait je me suis dit que puisqu'une série de Riemann \sum \frac{1}{n^{\alpha} converge ssi \alpha>1 , ça veut dire qu'il suffit d'être juste un peu plus "docile" que \sum \frac{1}{n} ...

j'en profite pour poser une autre question :id:
le critère de riemann est équivalent-il à "si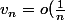 alors 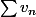converge" ?

hehe ça y est merci nightmare j'ai vu mon erreur !

Bonjour ! Je suis en train de me prendre la tête sur un question de développement limité et je n'arrive pas à voir où je me suis trompé ! On considère 4$u_n=\frac{n!e^n}{n^n\sqrt{n} et pour n>1 on pose 4$v_n=ln(u_n)-ln(u_{n-1}) . On veut le développement limité de v_n . Je trouve 4$v...

de toute façon ils peuvent pas le justifier puisque fourize n'a pas donné les bornes, on sait pas sur quel intervalle on intègre et si c'est bien défini =D

Zavonen a écrit:L'image de 1 par (1,2)(1,3) est 2
l'image de 1 par (1,3)(1,2) est 3
Les deux transformations ne sont pas identiques.

Je dirais que c'est plutôt l'inverse :we:

ah ui pardon j'avais considéré que le cas où detA>0 ^^'

hm pour n=2 c'est diagonal. Cas général moins évident ^^' surtout si c'est pas ça lol

a mon avis, ça tend vers \frac 1{z-1} Est ce que tu pourrais donner des indications sur cette conjecture ? =D ah l'erreur ! on ne devrait jamais donner de conseils tard le soir :) en tout cas, merci de ta vigilance ! hehe ben si ! ça fait avancer les choses un peu plus quand même ;) ce nouveau term...

Je pense que l'idée de Nightmare est le bon début, ainsi tu te ramènes à : 3$ a_p = \int_0^1(1-x)^{t/x}pe^{pz_px}dx et tu n'as plus que le terme pe^{pz_px} qui varie en fonction de p. Ensuite, il suffit de l'étudier et là pas besoin d'un truc aussi sophistiqué que la convergence dominée. Co...

j'ai oublié de préciser que Re(z)<1. J'ai édité mon premier post =) J'ai essayé avec cette majoration là aussi mais je ne sais pas si elle est assez fine. J'ai essayé (1-\frac{t}{p})^p\leq e^{-t} qui est pas trop mal puisque ça fournit un e^{-t} . Mais j'arrive pas à contrôler les e^{z_p t} ...

Nightmare a écrit:Salut!

Déjà je te suggère de poser x=t/p , vois-tu pourquoi?

Pour se ramener à une intégrale à bornes fixes ?

Bonjour tout le monde, Je sèche sur la limite suivante ^^' : 4$a_p=\int_0^p(1-\frac{t}{p})^pe^{z_p t}dt où (z_p)_{p>0} est une suite de complexes convergeant vers un complexe z de module inférieur ou égal à 1 et de partie réelle différente de 1. J'ai essayé le changement de variable ...

salut, en fait il s'agit d'une question de vocabulaire, de terminologie. Si on appelle R une relation d'ordre sur un ensemble E, X et Y des éléments de E. Si X R Y alors on dit que X "est plus petit que" Y pour R. Si par exemple X et Y sont des nombres réels, X R Y peut s'écrire X\leqY . S...

bonjour tout le monde ! J'ai l'impresssion que ça dépasse les notions que j'ai ^^'. Qu'entendez-vous par dimension d'un vecteur, le nombre de composantes non nulles ? Si le module est trop grand, je vois 2 cas: ou bien d>n et alors la somme a un rang au plus de d-1 et si jamais les composantes des v...