24 résultats trouvés
Revenir à la recherche avancée
Problème Probabilités
Bonjour, on a n cases numérotées de1 à n et on a 3 jetons qui portent les numéros 1,2 et 3 avec n\geq3 on pose au hasard le 1 sur l'une des cases numérotées de 1 à n-2.Soit i le numéro de la case où est posé le jeton 1 ensuite on pose le jeton 2 dans l'une des cases numérotées de i+1 à n-1.Soit j le...
- 30 Mar 2009, 21:07
- Forum: ✎✎ Lycée
- Sujet: Problème Probabilités
- Réponses: 0
- Vues: 499
dure equation!
Bonjou!
soit n de N tel que n 2
2
resoudre dans R l'equation:
}{cos^kx}}) =0
=0
Merci d'avance pour votre aide!
soit n de N tel que n
resoudre dans R l'equation:
Merci d'avance pour votre aide!
- 04 Mar 2009, 02:12
- Forum: ✎✎ Lycée
- Sujet: dure equation!
- Réponses: 1
- Vues: 309
Intégrales
Bonjour! on doit calculer la valeur moyenne de ces 2 fonctions: mais j'arrive pas a calculer son intégrale: I=[0,3] f(x)= \frac{e^{2x}-1}{e^{2x}+1} I=[0,1] f(x)= \frac{x^3+5x^2+x-3}{x+1} on doit trouver le fonctions primitives de ces 2 fonctions: I= \mathbb{R}_+^{\large\ast} f(x)=ln(x) I= \mathbb{R}...
- 25 Fév 2009, 19:28
- Forum: ✎✎ Lycée
- Sujet: Intégrales
- Réponses: 2
- Vues: 293
complexe
bonjour!
on pose x=
montrer que:
1+2x+3x²+...+1992x^1991=
merci d'avance!
on pose x=
montrer que:
1+2x+3x²+...+1992x^1991=
merci d'avance!
c'est bon pour la premiere question la lim c'est alpha tel que alpha la solution de l'equation x²lnx=1 mais pour les autres je ne sais pas toujours comment m'y prendre!merci en tout cas pour votre aide!
- 12 Déc 2008, 14:46
- Forum: ✎✎ Lycée
- Sujet: petites difficultés
- Réponses: 2
- Vues: 677
petites difficultés
bonsoir! je dois calculer la lim de Un on a (\forall n \in \mathbb{N}*) \exists! Un \in[\frac{1}{\sqrt{e}}, +linf[ : nf(un)-ne-1=0 et lequation x²lnx=1 admet une solution sur cet interval et aussi on a (Un) decroissante et convergente et f(x)= x^{x^2} , x>0 2eme question: soient a b et c des...
- 12 Déc 2008, 02:29
- Forum: ✎✎ Lycée
- Sujet: petites difficultés
- Réponses: 2
- Vues: 677
lim ln
bonsoir!
pouvez vous m'aider a resoudre ces 2 limites?
1-^{13}-8(lnx)^7+1}{(lnx)^9-4(lnx)^{13}+8})
2-^4}exp(\frac{1}{5-x}))
merci d'avance!
pouvez vous m'aider a resoudre ces 2 limites?
1-
2-
merci d'avance!
fonction
bonsoir!
on a=\left{2-\sqrt[3]{x^2+x+6}\text{ si } x \in [1,2[\\x+2-\sqrt{x^2-4}\text{ si } x\geq 2\right.)
il faut montrer que ( )
)  < f(x)<
< f(x)<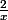
j'ai essayé la methode de derivation mais ca marche pas sauf erreur!!pouvez vous m'aider??merci !
on a
il faut montrer que (
j'ai essayé la methode de derivation mais ca marche pas sauf erreur!!pouvez vous m'aider??merci !
ln
bonsoir! on a n un entier naturel tel que n \geq 3 on considere la fonction g_n definie sur \mathbb{R}_+^{\large\ast} tel que: gn(x)=nx+2ln(x) 1-poser le tableau de variations de gn 2-montrer que ( \forall x \in \mathbb{R}_+^{\large\ast} ) \sqrt{x} > \ln(x) 3-montrer que l'equation gn(x)=0 a...
theoreme de ROLLE
bonjour! on a n un entier naturel tel que n \geq 2 et f une fonction continue sur [0,1] et derivable sur ]0,1[ tel que: f(0)=1 f(1)= \frac{2n}{2n-1} montrer que \exists c \in ]0,1[ : nf'(c)= \sqrt[n]{c^{n-1}} bon je penses qu'il faut utiliser ROLLE mais je ne trouve pas la fonction a poser!merci de ...
- 19 Nov 2008, 17:39
- Forum: ✎✎ Lycée
- Sujet: theoreme de ROLLE
- Réponses: 1
- Vues: 483
- 24 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
