Forum de Mathématiques: Maths-Forum

Bonjour,

J'ai écrit quelques formules et conjectures qui pourraient vous intéresser : http://squared.go.yj.fr/liste_formules_maths.png

N'hésitez pas à donner votre avis.

Bonsoir, J'ai soumis un article sur arxiv jeudi, ensuite dans la journée de jeudi le status de l'article était "incomplete" donc j'ai corrigé le fichier .tex Depuis jeudi soir mon article est en "on hold", il est dans la mauvaise catégorie mais c'est normal que ça prenne autant d...

J'ai modifié mon sujet en simplifiant la formule à démontrer (càd juste l'intégrale maintenant).

Pour répondre à vam : oui cette formule je l'ai trouvée avec l'aide de l'IA.

Bonjour,

Pour les formules je m'aide de l'IA mais je la corrige parfois.

Pour la conjecture précédente je ne me suis pas aidé de l'IA.

Bonjour,

J'aimerais démontrer la formule suivante.

---



Avec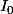 la fonction de Bessel modifiée de premier ordre.

---

Ah d'accord j'avais mal compris.
Sinon c'est qui ce Bill Dubuque ? Je pourrais peut-être le contacter.

stfj a écrit:Maintenant tu es à 11 sur mathoverflow

Merci si ça vient de toi.

J'ai envoyé ma conjecture à mon ancien prof de maths de terminale S (ça remonte à 2008 maintenant). Il m'a redirigé vers un maitre de conférence mais celui-ci est très occupé. Donc parfois je le relance mais il est occupé. C'est pour ça qu'on ne pourrait même pas en faire un exercice car pour démont...

Voici le lien mathoverflow (et j'avais 10 like pas 12) : https://mathoverflow.net/questions/4618 ... -of-primes

Ne tiens pas compte de car cette partie est fausse. Il faut tenir compte de .

Tu peux poser le problème sur Les-mathématiques.net ou, si l'anglais ne t'arrête pas, sur math stack exchange. Nul doute que ce problème en intéressera plus d'un. Je peux le faire à ta place si tu veux. Je l'avais déjà posé sur math stack exchange à l'époque, j'ai reçu 12 like mais ça dépassait tou...

Salut, A mon avis, vu que je ne pense pas qu'il y ait le moindre lien entre les propriétés (de congruence) d'un nombre premier p_n et son numéro n , pour qu'une telle conjecture ait (un peu) du sens, il faut commencer par remplacer le p_n par un p premier quelconque. Par contre, le \varphi(n...

Un autre exemple intéressant :

alors
Ici mais F(n) n'est pas premier donc on calcule Ici p=47 et k=6

Je ne sais pas pour quels on a . À première vue il me semble que cela soit aléatoire.

F(4)=\varphi(P_{6}-\sigma(6))+1=\varphi(13-12)+1=1+1=2 F(4) n'est pas congru à 3 modulo 20 donc on ne s'occupe pas de ce cas. F(8)=\varphi(P_{10}-\sigma(8))+1=\varphi(29-15)+1=\varphi(14)+1=6+1=7 Là encore une fois F(8) n'est p...

Non

Franchement je suis allé sur wolframalpha et sur calculis.net/premier pour tester si un nombre est premier ou s'il est une puissance de nombre premier.

Je l'ai trouvée un peu au hasard, on peut dire qu'il s'agit de sérendipité.

Non ce n'est pas moi qui l'ai testée jusqu'à plus de 500 000 000 mais quelqu'un qui l'a fait avec PARI/GP.
J'ai trouvé cette conjecture à force de bosser sur les nombres premiers. À mon humble avis elle n'existe pas dans la littérature mathématique.

Bonjour, Voici un exemple avec n=680 On a F(n)=\varphi(P_{682}-\sigma(680))+1=\varphi(5101-1620)+1=3423 3423 est congru à 3 modulo 20 mais n'est pas premier donc on calcule P_{682}-\sigma(680)=5101-1620=3481 Ici 3481 est la puissance d'un nombre premier, plus ...

Bonsoir, Je vous soumets un problème qui me bloque depuis plusieurs mois. --- Soit n un entier naturel supérieur à 1, \varphi(n) l'indicatrice d'Euler, P_n le nième nombre premier et \sigma(n) la somme des diviseurs de n. Soit l'expression F(n) = \varphi(P_{n+2}-\sigma...

Merci, je vais regarder ça.