5 résultats trouvés
Revenir à la recherche avancée
Re: Série entière
Et pour la 2) S= {\sum_{n=0}^{\infty}{(\frac{x^n}{2^n}})}={\sum_{n=0}^{\infty}{(\frac{x}{2}})^n}= \frac{1}{1-\frac{x}{2}} = \frac{1}{\frac{2-x}{2}} et elle existe lorsque {\frac{2-x}{2}}\neq 0\Rightar\Rightarrow 2-x\neq 0\Rightarrow x\neq 2 Donc S(x)= \frac{1}{\frac{2-x}{2}} avec x\n...
- 28 Fév 2024, 18:46
- Forum: ✯✎ Supérieur
- Sujet: Série entière
- Réponses: 7
- Vues: 248
Re: Série entière
D'accord je vois... Je me suis un peu embrouillé
Donc pour la question
1) est une série géométrique de raison
est une série géométrique de raison 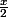 car
car 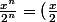^n) .
.
Elle converge si . Donc la série converge pour tout x<2
. Donc la série converge pour tout x<2
Donc pour la question
1)
Elle converge si
- 28 Fév 2024, 18:12
- Forum: ✯✎ Supérieur
- Sujet: Série entière
- Réponses: 7
- Vues: 248
Re: Série entière
Je suis un peu perdu (:
- 28 Fév 2024, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Série entière
- Réponses: 7
- Vues: 248
Re: Série entière
Bonjour Ben (:
Alors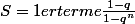
Mais je n'arrive pas à trouver la valeur de x pour laquelle S(x) existe
Alors
Mais je n'arrive pas à trouver la valeur de x pour laquelle S(x) existe
- 28 Fév 2024, 16:07
- Forum: ✯✎ Supérieur
- Sujet: Série entière
- Réponses: 7
- Vues: 248
Série entière
Bonjour à tout le monde, svp j'aimerais avoir de l'aide sur cet exercice si possible.. Merci d'avance On donne la série \sum{\frac{x^n}{2^n} 1) Pour quelle valeur de x la série converge-t-elle ? 2) Calculer lorsqu'elle existe la somme S(x)= {\sum_{n=0}^{\infty}{(\frac{x^n}{2^n}})} 3)Quel est...
- 28 Fév 2024, 12:58
- Forum: ✯✎ Supérieur
- Sujet: Série entière
- Réponses: 7
- Vues: 248
- 5 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
