Forum de Mathématiques: Maths-Forum

Personne pour me dire si ce que j'ai fait était juste?

J'ai dit que je venais de comprendre, c'est vrai, mais j'ai un souci pour les 2 autres cas. J'ai fait le cas ou a \geq 0 et b \leq 0 et je dois décomposer l'intégrale. J'ai dit que l'intégrale connair : \int_0^1( -x + \sqrt(2)yt dt) mais je pense que c'est faux. Et les mêmes calculs ...

Merci bien pour votre aide.

Maintenant, cela me parait très clair.

J'avais continué cet exercice et j'avais commencé à trouver quelques trucs.

Je viens d'effectuer les calculs, et j'ai remarqué qu'on avait bien 3 cas différents, mais je ne vois pas comment le généraliser avec x et y.
Enfin surtout comment je peux en déduire la boule unité.

Doit-on fixer x et y entre [-1,1]? Les 3 cas sont : 1/ \Large x+\sqrt{2}ty \geq 0 si \Large x \geq -sqrt{2}ty 2/ \Large x+\sqrt{2}ty \leq 0 si \Large x \leq -sqrt{2}ty 3/ \Large x+\sqrt{2}ty = 0 si x = -\sqrt{2}ty Mais je ne vois pas comment faire la suite. Doit-on calculer l'intégrale dans chaque c...

Pour fixer x et y : je définis par exemple x = t, et j'en déduis y.
Mais je ne vous pas la paramètrisation que je dois faire, j'ai essayé avec y =tx, x = ty, x = t, y = t, mais je n'ai rien trouvé de facile à exploiter.

Dans ce cas il faut que je calcul l'intégrale est seulement ensuite je formule mes conditions?

Non, je n'ai pas fait de dessin, je ne vois pas comment le faire d'ailleurs. On a \forall t \in [0,1] -1\leq x+\sqrt {2}ty\leq1 Sinon pour les 3 cas j'aurais donc : 1/ \Large x+\sqrt{2}ty \geq 0 si \Large x \geq -sqrt{2}ty 2/ \Large x+\sqrt{2}ty \leq 0 si \Large x \leq -sqrt{2}ty 3/ \Large x+\sqrt{2...

Dans ce cas il faut que je le fasse en fonction de t?

Ce qui donnerait :


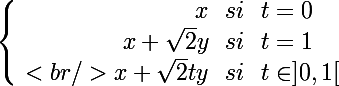
Et je détaillerais chaque cas?

Bonjour, J'aurais besoin de déterminer la boule : \Large{B =\{(x,y) \in \mathb{R^2} | N (x,y) \leq 1\}} avec \Large {N(x,y) = \int^1_0 |x + \sqrt{2}ty|dt} La valeur absolue me bloque, je ne vois pas comment m'en débarasser. Pourriez-vous me donner un coup de main? Merci d'ava...

J'ai essayé de faire le changement de variable mais je reste bloqué en fait. Je pensais qu'en faisant le changement de variable on avait : \large\int\frac{ch(x)}{2sh^2(x)}dx Mais en fait ce n'est pas dx mais d?. Et je ne vois pas ce que l'on peut mettre après le point d'interrogation.

En fait c'est bon j'avais pas vu au dessus que quand on changeais de variable il y a des expressions qu'on pouvait changer.

J'ai toujours un problème quand je veux faire l'intégrale par partie de chaque morceau.

La partie :



je ne peux pas la calculer.
Car ca me donne :

si tu sais ce que tu dois obtenir, dérive l'expression finale ? Je sais ce que je devais obtenir grâce à un site qui calcul les intégrales, mais sinon je n'aurais pas la réponse. bonjour 1 bonne idée de remettre les racines au numérateur 2 on calcule séparément chaque primitive par changement de va...

Bonjour, J'ai une intégrale à calculer qui me pose des problèmes. La voici : \large\frac{1}{\sqrt{{x}^{2}+1}+\sqrt{1-{x}^{2}}} J'ai essayé de le mettre sous la forme : \large\frac{\sqrt{{x}^{2}+1}-\sqrt{1-{x}^{2}}}{2\,{x}^{2}} Puis de faire une intégration par parties, mais je suis bloqué. Je sais l...

En fait c'est bon j'avais oublié la méthode.

Merci de votre aide.

Normalement je sais intégrer, et j'ai fais les équations différentielles, mais je ne vois pas comment on pourrait isoler que le y, puisqu'en intégrant sa primitive interviendra.

En fait, quand on intégre y''-y = 0, on obtient pas une forme connu, car on aura toujours une équation qui dépendra de y' et de la primitive de y. Donc on ne trouvera pas les solutions.

Oui je sais, mais dès fois je cherche trop compliqué en fait. Je pensais qu'il fallait le mettre sous la forme y''/y=1 ou -1, et j'essayais de trouver une formule que je connaissais.

Merci de votre aide.

Bonjour, Il y avait bien une erreur, le prof me l'a confirmé. J'ai avancé dans l'exercice mais je bloque encore sur une question. Entre temps j'ai montré que toutes les solutions, de cette équation différentielle, qui s'annulent en un point son identiquement nulle, et que si une autre fonction f est...