56 résultats trouvés
Revenir à la recherche avancée
"même si ce n'était pas agressif" Oui je le sais  Mais ce que je voulais dire par rapport à moi par contre, c'est que je n'aime pas trop toucher à ce qu'il y a dans les racines donc ici je n'ai pas chercher à factoriser par
Mais ce que je voulais dire par rapport à moi par contre, c'est que je n'aime pas trop toucher à ce qu'il y a dans les racines donc ici je n'ai pas chercher à factoriser par  dans la racine.
dans la racine.
- 15 Nov 2010, 19:32
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les limites
- Réponses: 11
- Vues: 480
Pour répondre à Sylviel, je ne comprends pas d'où tu sors cette idée comme quoi tous les jeunes sont des "shadocks", désolé mais je hais les préjugés, même si ce n'était pas agressif. Après c'est sûre que la solution pouvait être évidente mais n'ayant jamais vu une telle situation j'ai fais à ma man...
- 15 Nov 2010, 18:51
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les limites
- Réponses: 11
- Vues: 480
Justement, je cherche aussi une méthode plus simple, c'est d'ailleurs pour ça que je demande, désolé d'avoir était si peu clair.
Je cherche donc une méthode plus simple de résoudre ce problème.
Merci de vos réponses.
Je cherche donc une méthode plus simple de résoudre ce problème.
Merci de vos réponses.
- 14 Nov 2010, 23:44
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les limites
- Réponses: 11
- Vues: 480
Exercice sur les limites
Bonjour, J'ai un exercice que je crois avoir réussi mais je ne suis pas sûre de la méthode : Étudiez la limite en +\infty de : f(x) = \sqrt{x^2+1} - \sqrt{3x^2} \sqrt{x^2+1} - \sqrt{3x^2} = \frac{(\sqrt{x^2+1} - \sqrt{3x^2})(\sqrt{x^2+1} + \sqrt{3x^2})}{\sqrt{x^2+1} + \sqrt{3...
- 14 Nov 2010, 22:07
- Forum: ✎✎ Lycée
- Sujet: Exercice sur les limites
- Réponses: 11
- Vues: 480
- 13 Nov 2010, 20:49
- Forum: ✎✎ Lycée
- Sujet: Limite : Forme indéterminé
- Réponses: 5
- Vues: 1242
pour Joseph : J'ai multiplié comme tu m'as dis ça me donne : \frac{(x+2)\sqrt{x^2-x-6}}{(x+2)(x-1)-4} ce qui me donnerait donc comme limite 0 puisqu'on aura 0 en haut et 4 en bas. pour Mortelune : Je ne comprends pas comment tu veux que je factorise la racine à part avec \sqr...
- 13 Nov 2010, 14:38
- Forum: ✎✎ Lycée
- Sujet: Limite : Forme indéterminé
- Réponses: 5
- Vues: 1242
Limite : Forme indéterminé
Bonjour, Un exercice me demande : Étudiez la limite en -2 de f(x) = \frac{x+2}{\sqrt{x^2-x-6}} J'ai donc fais : Quand x tend vers -2 et x 0) \Longrightarrow \lim_{x \to 0} avec 0 > 0 de \sqrt{X} = 0 ( > 0) Mais je n'arrive pas à enlever la forme indéterminé après, ce n'est pas un taux d'accroissemen...
- 13 Nov 2010, 13:47
- Forum: ✎✎ Lycée
- Sujet: Limite : Forme indéterminé
- Réponses: 5
- Vues: 1242
Ok je comprends.
1er point : si z est sur la droite y = x - 2 alors Z = i(x - 2 - (x - 2)) + (x - 3) = 0 + x - 3 donc Z est un réel.
Par contre je ne comprends pas le deuxième point : Im(z) veut bien dire image de z? et Re(z) réel de z? Si c'est le cas, je dois chercher les coordonnées de z?
1er point : si z est sur la droite y = x - 2 alors Z = i(x - 2 - (x - 2)) + (x - 3) = 0 + x - 3 donc Z est un réel.
Par contre je ne comprends pas le deuxième point : Im(z) veut bien dire image de z? et Re(z) réel de z? Si c'est le cas, je dois chercher les coordonnées de z?
- 11 Nov 2010, 20:14
- Forum: ✎✎ Lycée
- Sujet: Problème de rédaction
- Réponses: 2
- Vues: 983
Problème de rédaction
Bonjour, j'ai souvent des problèmes de rédaction et ici c'est assez important. J'ai trouvé la réponse mais je ne sais pas formulé la déduction : "z = x + iy avec x et y réels. On note Z le nombre complexe Z = iz + \bar{z} - 3 - 2i. 1/ Vérifiez que Z - \bar{Z} (expression conjugué de Z pas de z ...
- 11 Nov 2010, 19:11
- Forum: ✎✎ Lycée
- Sujet: Problème de rédaction
- Réponses: 2
- Vues: 983
- 10 Nov 2010, 17:07
- Forum: ➳ Orientation
- Sujet: Ingénieur
- Réponses: 3
- Vues: 914
Ingénieur
Bonjour,
Je voulais savoir quelle type de maths était principalement vu en Ingénieur par rapport au programme de Terminale S (Spé maths inclus)?
Merci et au revoir.
Je voulais savoir quelle type de maths était principalement vu en Ingénieur par rapport au programme de Terminale S (Spé maths inclus)?
Merci et au revoir.
- 08 Nov 2010, 22:57
- Forum: ➳ Orientation
- Sujet: Ingénieur
- Réponses: 3
- Vues: 914
- 01 Nov 2010, 23:45
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
- 31 Oct 2010, 15:41
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
Oui mais si tu regardes la question A)3) "Déduisez-en que toute équation du troisième degré admet au moins une solution dans ." Le but c'est de justement montrer que la continuité on l'a sur une fonction polynôme du troisième degré.
- 31 Oct 2010, 14:24
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
Pour le A)2) j'ai finalisé en disant : On en déduit que f(x) est une fonction continu car lorsque x tend vers - ou
ou  , f(x) tend vers -
, f(x) tend vers - ou
ou  donc
donc 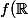 = \mathbb{R}) .
.
Est-ce que c'est complet?
Merci pour vos réponses.
Est-ce que c'est complet?
Merci pour vos réponses.
- 31 Oct 2010, 11:32
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
De toute façon j'ai trouvé la réponse avec la première aide de Arnaud :) j'avais juste pas compris un point. Mais je sais qu'il faut que je démontre qu'elle est unique d'abord avec ce que j'ai fais et ensuite le TVI (théorème de la bijection si tu préfères c'est la même chose) et ensuite à la questi...
- 31 Oct 2010, 10:39
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
Salut "Pour f(R) = R, il faut utiliser l'argument que f(x) tend vers en et vers en pour a > 0 (et vice versa pour a < 0). Il faut ensuite ajouter la continuité." J'ai fais ça déjà mais je bloque justement quand il faut ajouter la continuité, je trouve ça abstrait et je ne comprends pas exa...
- 30 Oct 2010, 18:57
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
Exercice sur la continuité
A: f est la fonction définie sur \mathbb{R} par : f(x) = ax^{3} + bx^{2} +cx +d où a, b, c et d sont quatre réels (a différent de 0) 1) Étudiez suivant le signe de a, la limite en +\infty et en - \infty de f(x). Ici pas trop de problèmes, je vous épargne les détails mais si ça peut aider pou...
- 30 Oct 2010, 16:38
- Forum: ✎✎ Lycée
- Sujet: Exercice sur la continuité
- Réponses: 17
- Vues: 950
Tout simplement parce que le livre d'exercice a qualifié cet exercice de difficile alors que d'autres plus difficile sont qualifiés de normaux, enfin bon, au moins je suis sûre de ce que j'ai fais :)
- 10 Oct 2010, 22:01
- Forum: ✎✎ Lycée
- Sujet: Exercice de Congruences
- Réponses: 4
- Vues: 580
- 10 Oct 2010, 19:10
- Forum: ✎✎ Lycée
- Sujet: Exercice de Congruences
- Réponses: 4
- Vues: 580
- 56 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
