Bonjour,
Petit défi : chercher (et trouver !) une preuve directe (sans récurrence).
Je ne l'ai pas pour l'instant mais je pense que c'est faisable (probablement pas facile).
P.S. Le site ne marche pas bien : j'ai eu un mal de chien à poster avec des "erreurs" en pagaille.
8 résultats trouvés
Revenir à la recherche avancée
- 28 Mar 2024, 14:26
- Forum: ⚔ Défis et énigmes
- Sujet: Somme des inverses des coefficients binomiaux
- Réponses: 15
- Vues: 875
Re: Somme des inverses des coefficients binomiaux
Bonjour à tous, Je retranscris ici la démonstration de la formule de récurrence "délicate" telle que je l'avais écrite "ailleurs" il n'y a pas loin de 6 ans : S_n=\sum_{k=0}^n\dfrac{1}{\binom{n}{k}} S_{n+1}=\sum_{k=0}^{n+1}\dfrac{1}{\binom{n+1}{k}}=1+\sum_{k=0}^n\dfrac{k!(n+1...
- 27 Mar 2024, 18:45
- Forum: ⚔ Défis et énigmes
- Sujet: Somme des inverses des coefficients binomiaux
- Réponses: 15
- Vues: 875
Re: Somme des inverses des coefficients binomiaux
Bonjour,
On peut montrer que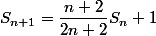 (c'est le plus délicat).
(c'est le plus délicat).
Puis par récurrence que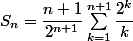
On peut montrer que
Puis par récurrence que
- 27 Mar 2024, 14:23
- Forum: ⚔ Défis et énigmes
- Sujet: Somme des inverses des coefficients binomiaux
- Réponses: 15
- Vues: 875
Re: Intégrale impropre
Bonjour, A l'infini, il n' y a pas grand problème et en 0 tu peux obtenir un équivalent de l'intégrande. Quant au calcul, une intégration par parties marche bien. On trouve \pi . [Edit] J'ajoute que poster deux fois la même demande n'est pas tellement apprécié. Et que dire de ceci : https://les-math...
- 26 Juin 2023, 12:13
- Forum: ✯✎ Supérieur
- Sujet: Intégrale impropre
- Réponses: 1
- Vues: 250
Re: calculer la distance d'un point avec une parabole
Bonjour, Ce problème de distance minimale d'un point à une conique mérite quelques développements : Dans l'équation de la parabole proposée, \alpha représente l'angle de son axe et de l'axe des ordonnées. On peut récupérer son foyer F et sa directrice \Delta . Le problème consiste à chercher les poi...
- 25 Juin 2023, 16:06
- Forum: ✯✎ Supérieur
- Sujet: calculer la distance d'un point avec une parabole
- Réponses: 5
- Vues: 392
Re: Résolution d'une équation
Bonjour,
J'ai ravalé ma réponse suite à celle de lyceen95
Une précision :
A priori il n'y en a que deux.
J'ai ravalé ma réponse suite à celle de lyceen95
Une précision :
un "calcul simple" permet de déterminer les trois solutions.
A priori il n'y en a que deux.
- 24 Juin 2023, 09:27
- Forum: ✯✎ Supérieur
- Sujet: Résolution d'une équation
- Réponses: 3
- Vues: 248
Re: Calcul du volume d'intersection entre un pavé et un cône
Bonjour, Le pavé est défini par son centre O et les trois dimensions de ses côtés. Le cône est défini par son sommet P, le vecteur unitaire directeur G de sa hauteur, et le demi angle alpha entre la hauteur et le cône. Il manque la position relative du cône et du pavé pour préciser le volume en ques...
- 21 Juin 2023, 12:13
- Forum: ✯✎ Supérieur
- Sujet: Calcul du volume d'intersection entre un pavé et un cône
- Réponses: 7
- Vues: 410
Re: Exercice de maths sur les cercles et les tengentes
Bonjour, Une solution alternative consiste à déterminer les centres I et J des homothéties (positive et négative) qui permettent de passer d'un cercle à l'autre. \dfrac{\overline{IO_2}}{\overline{IO_1}}=-\dfrac{\overline{JO_2}}{\overline{JO_1}}=\dfrac{4}{9} I barycentre de \{(O_1,4);(O_2...
- 17 Juin 2023, 13:05
- Forum: ✯✎ Supérieur
- Sujet: Exercice de maths sur les cercles et les tengentes
- Réponses: 5
- Vues: 462
- 8 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
