Forum de Mathématiques: Maths-Forum

Salut

Avec les notations précédentes, la probabilité d'avoir une rupture de stock un mois donné est p = P( X < 0 ) = P ( < ?) où tu dois calculer la valeur ?

Tu as raison : si tu poses une variable aléatoire N qui désigne le nombre de ruptures de stock sur les trois mois, elle suis bien une loi binomiale B(3;p) où p est la probabilité d'avoir une rupture de stock. Pour calculer cette probabilité, tu dois utiliser les propriété de la loi normale. Le stock...

Tu cherches P( X < 0 ).
Si tu centres et réduis, qu'obtiens tu ?

L'endomorphisme f possède trois valeurs propres distinctes (en dim 3 ), et c'est sur ce point qu'il faut travailler pour résoudre la question 2.
Les deux endomorphismes seront dits simultanément diagonalisables s'il existe une base au sein de laquelle ils sont tous deux diagonalisables.

Salut

Dans le théorème de diagonalisation simultanée, il faut que f et g soient diagonalisables et commutent.
Ton hypothèse manquante ne serait-elle pas que g est diagonalisable ?

Pour les formules avec 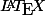, va voir le lien : http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php

Salut Pour la question 2, une condition nécessaire à $ l \in \mathbb{R} \cup \{ \infty \} $ pour être une limite est de vérifier l'équation $ l = \frac{1}{2} (l^2 + l^2) $ ; pour s'en convaincre, il suffit de faire la limite en l'infini de l'égalité définissant la suite. Pour les limites inf...

Donc cela convient uniquement pour les endomorphismes. Merci

Bonjour,

Soit une application linéaire entre deux espaces de dimension finie.
Si l'application est injective, est-il indispensable de vérifier que le dimension des deux espaces est la même pour conclure qu'elle est bijective ?

Merci d'avance

Salut http://img571.imageshack.us/img571/6397/trapze.png Sur la figure, il semblerait que la droite cherchée est la parallèle passant par I à la droite ou D "navigue". Je suppose que cet exercice est en lien avec un cours sur les vecteurs. Soit D1 un point de la droite (d) que décrit D et ...

Salut Le terme ''suite réciproque'' semble très aventureux ! Tu sembles penser à faire une étude de cas pour monter que l'image de tous nombre est 213, c'est une bonne idée. Je n'aurais pas utilisé la notation littérale de arnaud mais elle est sympa. Attention à bien étudier tous les cas. x(33333333...

Salut Le symétrique du numérateur est le dénominateur. Comme tu viens de trouver le symétrique de quatre chiffres différents, il te suffit d'en choisir deux pour trouver le symétrique dont le numérateur est une nombre à deux chiffres tous différents. Par exemple : 50/?? De même pour la deuxième ques...

Salut Pour le tirage a), on utilise des combinaisons car c'est un tirage simultané, donc pour 1a) c'est bon. Pour 2a), il me semble que ton dénominateur est imprécis. Tu n'as pas calculé le nombre de tirages de deux cartes mais d'une seule. (Ce dénominateur est le même qu'au 1a) ) Pour le tirage b),...

Bonjour Voici un exercice : Le plan euclidien étant rapporté à un repère orthonormé (O;i ;j ), on considère le cercle C (resp. C0) de centre A(R; 0) (resp. A0(R0; 0)) et de rayon R (resp. R0). Un point M (resp. M0) décrit le cercle C (resp. C0). Le but de l’exercice est de déterminer le maximum de l...

La question qui nous intéresse est : en déduire l'existence d'une famille de polynômes (Pi) vérifiant l'égalité. Cela veut dire qu'il ne faut pas nécessairement préciser ces solutions. As tu en cours, fait le lien entre le matrice et système linéaire d'équations définie par cette matrice ? Ici c'est...

L'astuce du (y+1)^n - y^n est que les termes de degré n s'annulent.

On regarde donc les termes de degré n-1 de (y+1)^n - y^n et de (y-1)^n - y^n.
Quels sont-ils ?

C'est ça.
On note ces racines aussi j et j².

Je pense que la forme exponentielle est celle qui permet le mieux de résoudre Z^4=c ou c est un complexe donné

Je voyais plutôt la formule dans le sens développer (a+b)^n

Tu peux poser Y=X^4 et factoriser le polynôme en Y

Salut,

Je pense qu'on peut aboutir directement avec la formule du binôme de Newton.
Qu'as tu écrit ?

Pense aussi qu'on ne s'intéresse pas à tous les termes mais que l'on cherche le terme de plus haut degré dont le coefficient est non nul.