36 résultats trouvés
Revenir à la recherche avancée
- 05 Fév 2009, 20:35
- Forum: ✯✎ Supérieur
- Sujet: Fonction de réparition de inf(X1, ..., Xn)
- Réponses: 2
- Vues: 417
Fonction de réparition de inf(X1, ..., Xn)
Bonjour, je voulais savoir si l'on pouvait dire que, lorsqu'on a Y = inf(X1, ..., Xn), pour tout t de R, Fy(t) = inf ( Fx1(t) ; ... ; Fxn(t) ) ?
(Je sais que ce n'est pas très pratique et que lorsqu'il y a indépendance, il faut passer par les intersections...).
Merci d'avance.
(Je sais que ce n'est pas très pratique et que lorsqu'il y a indépendance, il faut passer par les intersections...).
Merci d'avance.
- 05 Fév 2009, 17:59
- Forum: ✯✎ Supérieur
- Sujet: Fonction de réparition de inf(X1, ..., Xn)
- Réponses: 2
- Vues: 417
Sur mon dernier post, je me suis trompé dans le somme. Mais sinon j'ai repris du début le calcul, et ça semble marcher. Petite question : lorsque je dérive ma relation 4$ \sum_{k=0}^n \left(\begin{array}{c} n \\ k\end{array}\right) X^k(1-X)^{n-k} = 1 j'ai bien une somme qui va de k =...
- 11 Jan 2009, 23:59
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une somme
- Réponses: 12
- Vues: 1415
aloha, grosso modo calcul de G(Y) = \sum Y^k (progression géométrique) on dérive G'(Y) = \sum kY^{k-1} on multiplie par Y YG'(Y) = \sum kY^k dans la somme initiale, on factorise (1-X)^n on fait un changement de variable Y = \frac{X}{1-X} avec coeff binomiaux,...
- 11 Jan 2009, 22:25
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une somme
- Réponses: 12
- Vues: 1415
- 11 Jan 2009, 21:41
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une somme
- Réponses: 12
- Vues: 1415
- 11 Jan 2009, 21:28
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une somme
- Réponses: 12
- Vues: 1415
Calcul d'une somme
Bonjour, j'aurais besoin d'aide pour le calcul d'une somme :
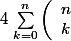 kX^k(1-X)^{n-k})
Des pistes?
Merci d'avance.
Des pistes?
Merci d'avance.
- 11 Jan 2009, 21:27
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une somme
- Réponses: 12
- Vues: 1415
Demande de confirmation d'une matrice sur C^3
Bonjour, dans mon dm, à une question, je dois trouver une matrice et je ne suis pas sûr de mon résultat, c'est pourquoi je fais appel à votre aide... Désolé si l'énoncé est un peu long et on s'y perd un peu au début. On travaille dans le cas particulier n=3. On travaille sur l'espace vectoriel C^3 s...
- 03 Jan 2009, 18:39
- Forum: ✯✎ Supérieur
- Sujet: Demande de confirmation d'une matrice sur C^3
- Réponses: 1
- Vues: 764
Oui et lorsque d'une application g appartient à T (E) et à L (E), l'application est anti-symétrique...
- 07 Déc 2008, 15:45
- Forum: ✯✎ Supérieur
- Sujet: Déterminer une base
- Réponses: 2
- Vues: 790
Déterminer une base
Bonjour, mon problème est que j'ai un espace vectoriel L (E) ;) T (E) et que je dois en trouver une base. (je tiens à souligner que E est un e.v. euclidien de dim n, dont le produit scalaire est <.|.>, L (E) l'ensemble des endomorphismes de E et que T (E) est l'ensemble des applications f de E qui v...
- 07 Déc 2008, 12:23
- Forum: ✯✎ Supérieur
- Sujet: Déterminer une base
- Réponses: 2
- Vues: 790
nuage a écrit:Salut,
pour tirer n boules noires en n+k tirages il faut avoir pris exactement k boules boules blanches en n+k tirages.
Je ne vois pas où introduire une loi hypergéométrique.
Sommes-nous bien d'accord qu'on effectue des tirages sans remise?
- 13 Nov 2008, 23:37
- Forum: ✯✎ Supérieur
- Sujet: Trouver la loi d'une VAR discrète
- Réponses: 4
- Vues: 735
Trouver la loi d'une VAR discrète
Bonsoir, je suis confronté à une exercice de probabilité : une urne contient n boules blanches et n noires, On effectue des tirages consecutifs sans remise, X est le nombre de tirages nécessaires pour qu'il ne reste plus de boule noire. Il faut trouver la loi de X. Tout d'abord on sait que X est à v...
- 13 Nov 2008, 23:06
- Forum: ✯✎ Supérieur
- Sujet: Trouver la loi d'une VAR discrète
- Réponses: 4
- Vues: 735
Ok j'ai quelque chose : avec t=1-u; g(x)=e.\int_{1-x}^{+\infty}\frac{e^{-t}}{t}dt puis faire une IPP...cette fois ca marche bien :we: J'ai appliqué le changement de variable t = 1-u, puis une IPP. Après l'intégrale issue de l'IPP tend vers 0 en - infini. Il nous reste donc notre "u(t)....
- 19 Oct 2008, 16:00
- Forum: ✯✎ Supérieur
- Sujet: Montrer la négligeabilité d'une intégrale devant exp(x)
- Réponses: 9
- Vues: 1473
- 19 Oct 2008, 15:27
- Forum: ✯✎ Supérieur
- Sujet: [résolue] (Nouvelle) demande de confirmation de la divergenc
- Réponses: 8
- Vues: 939
e^{-t} tend vers quoi en 0 ? Donc \frac{e^{-t}}{t}\sim\limits_{0} à quoi ? e^{-t} tend vers 1 en 0, donc \frac{e^{-t}}{t}\sim\limits_{0} \frac{1}{t} .... Merci. Mais en fait, hier soir dans mon post j'avais proposé la même chose en faisant \frac{e^{-t}}{t}\sim\limits_{0} \frac{1}{t} , on m'a dit qu...
- 19 Oct 2008, 15:19
- Forum: ✯✎ Supérieur
- Sujet: [résolue] (Nouvelle) demande de confirmation de la divergenc
- Réponses: 8
- Vues: 939
En posant, t = a - u, on a }{a-u}du) =
=  \bigint_{0}^{1} \frac{exp(-t)}{t}dt)
Ensuite,) est négligeable devant 1/t en 0. { je doute de la véracité de ce passage}
est négligeable devant 1/t en 0. { je doute de la véracité de ce passage}
...
...
On en conclue que notre intégrale n'existe pas.
Ensuite,
...
...
On en conclue que notre intégrale n'existe pas.
- 19 Oct 2008, 15:01
- Forum: ✯✎ Supérieur
- Sujet: [résolue] (Nouvelle) demande de confirmation de la divergenc
- Réponses: 8
- Vues: 939
tize a écrit:Désolé j'ai bouletté :briques: je regardai en +infty
Bon je cherche
J'avais fait la même erreur avec mon encadrement au début, mais j'me suis rendu compte en me relisant hier que c'était faux.
- 19 Oct 2008, 14:51
- Forum: ✯✎ Supérieur
- Sujet: Montrer la négligeabilité d'une intégrale devant exp(x)
- Réponses: 9
- Vues: 1473
tize a écrit:Oui mais il n'y a pas d'indetermination...donc en résumé g(x) tend vers 0 en -l'infini etaussi donc
tend vers ?...
Non,
- 19 Oct 2008, 14:47
- Forum: ✯✎ Supérieur
- Sujet: Montrer la négligeabilité d'une intégrale devant exp(x)
- Réponses: 9
- Vues: 1473
Justement, j'ai un peu de mal dans les bornes de l'intégrale avec les changements de variables, et à finaliser le tout.
Est-ce que je peux écrire mon raisonnement pour voir s'il n'y pas d'incohérence?
Est-ce que je peux écrire mon raisonnement pour voir s'il n'y pas d'incohérence?
- 19 Oct 2008, 14:45
- Forum: ✯✎ Supérieur
- Sujet: [résolue] (Nouvelle) demande de confirmation de la divergenc
- Réponses: 8
- Vues: 939
En - infini, cette intégrale tend vers 0.
On se retrouve avec un indétermination entre l'exponentielle et l'intégrale, sauf si on peut étudier ça, mais je ne vois pas comment.
On se retrouve avec un indétermination entre l'exponentielle et l'intégrale, sauf si on peut étudier ça, mais je ne vois pas comment.
- 19 Oct 2008, 14:36
- Forum: ✯✎ Supérieur
- Sujet: Montrer la négligeabilité d'une intégrale devant exp(x)
- Réponses: 9
- Vues: 1473
- 36 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
