Forum de Mathématiques: Maths-Forum

Merci avec ça je ne devrais pas avoir de problème avec la suite (même si j'ai plus vraiment le temps de le faire ^^).

ça devait être un problème de compréhension de l'énoncé car en effet j'ai calculé Ep(X) comme étant Ep(x/b). Donc la variable X est muette dans Ep(X) (donc Ep(x)=Ep(X)?) mais est égale à x/b dans V(X)? Ça me parait étrange mais c'est en effet le seul moyen qui conviendrait pour factoriser Ep(x) par ...

je me suis trompé dans mon poste précédent je voulais écrire: Ep(X)= kb^2\alpha( \frac {x^2} {\alpha b^4} +2 (1- sqrt {1+ \frac {x^2} {b^4}}) pour la factorisation je ne vois pas ce qui cloche, j'ai fais: Ep(x)=k(\frac {x^2}{2}+lo.b(1-\sqrt {1+\frac {x^2}{b^2}}...

d'abord merci d'avoir "sacrifié" ton premier message (deux fois, ce qui est assez paradoxal...) pour me répondre c'est très sympathique de ta part. En effet en factorisant Ep(x) par b^2 et alpha j'obtiens (en prenant Ep(x) double puisqu'il semblerait que je me soit trompé). Ep(x)= ...

c'est en effet ce que tu dois faire mais ton équation risque d'être un polynôme du second degré en quel cas il te suffirait d'utiliser le discriminant etc, bonne chance.

disons que tout antécédent de la fonction exponentielle admet une seule image (car elle est strictement croissante sur R), donc e^x=a admet une seule solution il faut donc te ramener à une equation de cette forme. et pour l'equation f(x)-x= (-x.e*x)/(e*x+1) que tu as trouvée il te suffit de factoris...

ok (désolé pour toute cette confusion), je suis plus très à jour sur le théorème de la bijectivité mais en gros tu dois dire que e^{x} réalise une bijection de \mathbb{R} sur \mathbb{R}_+^* et donc que toute valeur de l'ensemble d'arrivé est atteinte une et une seule fois donc il existe une seul sol...

je vais paraitre idiot mais je n'arrive pas à comprendre ce que veux dire ton e*x-1...est-ce:


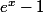
ou e fois x-1 (en quel cas est ce que e est une constante?)

est ce que ex-1 veut dire ou juste e*x-1

résoudre ce système ne te donnera pas un couple de coordonnées mais au mieux un ensemble de couples qui dépendent de t (puisque tes équations dépendent de t), si c'est ce que tu cherches il te suffit de résoudre l'équation donnée par Arka en x puis d'injecter dans une des équations de ton système (a...

....je l'avoue, j'ai relu mon cours en vitesse avant de poster ma réponse, je suis pas non plus tout à fait au point :p

je ne crois pas qu'il ait réellement de nom, on dit juste que l'exponentielle est plus forte ou prédomine sur la puissance de x (ou on redémontre vite fait si besoin est).

un indice :

Bonjour ( vous avez peut être apercu ce topic plusieurs fois déjà et pour cause il a été supprimé plusieurs pour avoir enfreint le règlement), j'ai passé plus d'une heure sur le début de ce DM qui ne semble d'ailleurs pas difficile et pourtant je bloque, mes résultats ne coïncident pas. Voici le suj...

Tu n'es pas censé donner la réponse !

Le reste est bon

merci beaucoup, en effet je n'ai pas encore vu les équations cartésiennes mais bon je vais voire ce que je peux en faire, sinon pour trouver f(0) je pose juste k= -;)2+1/(1/(2;)2) + k) et je résout ça? Dans ce cas je ne vois pas vraiment à quoi sert l'indice donné dans l'énoncé.

Merci pour ta réponse mais pour la première question je suis sûr que ma solution complète de (E) est bonne (mathematica et la quasi-totalité de ma classe sont d'accord)cependant je ne sais pas comment prouver son unicité (ni comment faire la suite) ni même comment définir son ensemble de définition....

bonjour, je suis nouveau sur ce site mais je risque d'y passer une bonne partie de mon temps car j'entre en première année de MPSI et c'est vraiment pas facile :triste: . J'essaierais aussi bien entendu d'aider les autres autant que possible mais là j'ai vraiment besoin d'aide sur un DM (pour jeudi,...