Forum de Mathématiques: Maths-Forum

Euh oui, je me suis trompé là, en recherchant j'ai trouvé les équation : \left\{ \begin{array} x = \frac{ax_A+bx_B+cx_C}{a+b+c} \\ y = \frac{ay_A+by_B+cy_C}{a+b+c} \\ z = \frac{az_A+bz_B+cz_C}{a+b+c} \end{array} \right. Merci de vos réponses. Je ne comprends pas ce qui ne va pas, une fois implémenté...

PS : je viens de voir que c'était pour un algo, tu voudras sans doute avoir une paramétrisation canonique du cercle, auquel cas il vaut mieux prendre IA et un vecteur orthogonal à IA (à la place de IB dans mon exemple), comme IB-(IB.IA)IA/|IA|². Pour calculer le vecteur orthogonal la formule est bi...

D'accord, merci.

Maintenant, Si le problème est inverse, on cherche à trouver un point qui vérifie cette propriété, comment faire ?

chan79 a écrit:Pour savoir si un point M appartient au cercle, on pourrait voir si le déterminant des trois vecteurs , et est nul et si IM=r

Si j'ai bien compris, il faut faire le produit mixte des vecteurs qui nous indique si le point M est dans le plan.

Bonjour, Dans le but d'implémenter un algorithme, je cherche à calculer le cercle inscrit dans un triangle. Trouver le centre est simple, pour un triangle ABC le centre I du cercle aura comme coordonnées I = \frac{A+B+C}{3} . Le rayon r du cercle se calcule en faisant r = \frac{2S}{a+b+c} où a b et ...

Ah, il me semblait avoir dit dans mon premier message qu'on connaissait n, pet q tel que n=pq , désolé si je n'ai pas été clair. Du coup on connait \Phi(n) , donc la il ne me reste plus qu'à exécuter l'algorithme d'Euclide pour trouver k et d dans ed - k\Phi(n) = 1 merci de tes répon...

Donc si j'ai bien comprit on a , j'ai bien peur de n'avoir pas saisi le résonement qui pourrait m'amener à la réponse.

Bonjour, Tout d'abord merci de vos réponses, j'ai toutefois des questions à poser. Si x^{de} \equiv x \pmod{n} peut on en déduire que de \equiv 1 \pmod{n} ? Si oui il faut donc trouver l'élément inversible de e pour trouver la valeur de d, il faut donc poser e \times a + n \times b = 1 comment trouv...

Bonjour, Mon sujet porte sur le décryptage d'une chaîne cryptée par RSA. Soit x le message la fonction publique qui code le message est : f(x) \equiv x^e \pmod{n} Pour décoder le message la fonction est : f^{-1}(x) \equiv x^d \pmod{n} Il nous faut donc trouver d. On connait x^e , e e...

Bon, et bien le problème venait de moi, je n'avais pas vu que dans l'énnoncé il y avait 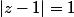et don lorsque je suis arrivé à j'aurais du simplifier par un et j'aurai trouvé la bonne réponse, parfois la résolution d'un exercice de maths c'est simple comme d'ouvrir les yeux.

Ah si t'as jamais eu dans tes cours le signe auquel je pensais tu pouvais pas l'inventer, pour f(x)>0 : x;)[1;4] j'ai jamais vu cette notation mais si dans ton cours elle est présente elle est surement juste.

PS: je pensait à

C'est presque ça, il manque un signe devant pour dire "pour tout" et le alors il me semble que c'est la double flèche se dirigeant vers ton inéquation.

Tout juste auguste

Je vais reformuler en français, tu trouveras surement :

pour tout x appartenant à l'intervale [1;4] alors la fonction de x est supperieure à 0.

Il manque une partie de la réponse, il faut que tu dises sur quel intervale ton inéquation est juste.

Je ne comprend pas là où tu veux en venir, il faut que je prouve l'égalité pour toute les valeurs de z et z'. Si je prend un nombre arbitraire pour une démonstration, il faut que je prouve pour l'infinité de nombre qu'il reste autant dire que je ne suis pas couché ... Je sens qu'il faut que je me se...

Il ne s'agit pas de Z' mais de |z'|, de son module.

Il faut que tu dises que pour toute les valeurs de x comprises dans l'intervale, f(x) est supperieur à 0, tu trouveras en cherchant dans tes cours, les symboles qui expriment cette phrase en language mathématiques.