Pour information , cet exercice a été donné à l'oral de Centrale 1933 !
La résolution d'une équation du troisième degré étant complexe ,Je pense qu'il fallait donner le résultat en fonction de a sans chercher une valeur numérique.
25 résultats trouvés
Revenir à la recherche avancée
- 21 Jan 2025, 19:20
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
Avec mes notations l'intégrale donne : \int_{0}^{-a}\frac{dx}{x^{3}+x+1}=\frac{1}{3a^{2}+1}\left( ln(2)+\frac{6a}{\sqrt{3a^{2}+4}}*arctg(\frac{a}{\sqrt{3a^{2}+4}}) \right)=0.499 ! Je vais me résoudre à admettre cette valeur approchée bien que je pense que la valeur exacte est...
- 08 Jan 2025, 16:55
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
Je ne comprend pas trop le raisonnement de Phyelec :
A,B,C sont arbitraires ?
Au final cela donne quoi ?
A,B,C sont arbitraires ?
Au final cela donne quoi ?
- 08 Jan 2025, 10:50
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
J’ai calculé la primitive pour une valeur de a = - 0.6823. Cela me donne comme résultat pour l’intégrale la valeur 0.4993. Je pense que la solution cherchée est ½ ( confirmée par un graphique Géogebra ), mais je ne sais pas le montrer… Il,y a probablement une méthode élégante sans passer par la prim...
- 05 Jan 2025, 18:52
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
Il y a une seule racine réelle , x2 et x3 sont des racines complexes...
- 04 Jan 2025, 18:36
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
Oups , je pense que la décomposition en facteurs de catamat est fausse ....
Ce serait plutot (x-a)(x²+ax + a²+1)
Ce serait plutot (x-a)(x²+ax + a²+1)
- 02 Jan 2025, 19:19
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: intégrale définie
OK pour calculer une primitive , mais comment tenir compte du fait que le paramètre a est racine d'une équation du troisième degré ?
- 01 Jan 2025, 16:45
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
intégrale définie
Bonjour à tous et bonne année !
Quequ'un peut il m'aider à résoudre l'exercice suivant ?

Quequ'un peut il m'aider à résoudre l'exercice suivant ?
- 01 Jan 2025, 12:16
- Forum: ✯✎ Supérieur
- Sujet: intégrale définie
- Réponses: 16
- Vues: 2146
Re: Croisement d'ellipses
merci Gabuzomeu c'est la formule élégante que j'attendais !
- 27 Jan 2023, 16:11
- Forum: ✯✎ Supérieur
- Sujet: Croisement d'ellipses
- Réponses: 7
- Vues: 389
Re: Croisement d'ellipses
Oups une petite erreur ... il faut lire !
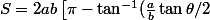 -\tan^{-1}(\frac{a}{b} \cot {\theta /2}\right)])
- 27 Jan 2023, 11:08
- Forum: ✯✎ Supérieur
- Sujet: Croisement d'ellipses
- Réponses: 7
- Vues: 389
Re: Croisement d'ellipses
Bonjour,
Après prise en compte des symétries , j'arrive à la formule ultime suivante qui fonctionne pour les cas particuliers theta =pi/2 et theta =0 :
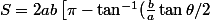 -\tan^{-1}(\frac{b}{a} \cot {\theta /2}\right)])
Si quelqu'un a mieux ....
Après prise en compte des symétries , j'arrive à la formule ultime suivante qui fonctionne pour les cas particuliers theta =pi/2 et theta =0 :
Si quelqu'un a mieux ....
- 27 Jan 2023, 11:04
- Forum: ✯✎ Supérieur
- Sujet: Croisement d'ellipses
- Réponses: 7
- Vues: 389
Re: Croisement d'ellipses
bonjour a et b étant fixés, je cherche une formule donnant l'aire en fonction de theta. Pour cela , je pars de l'équation polaire des ellipses : \rho ^{2}=\frac{1}{\frac{cos^{2}(\varphi -\theta )}{a^{2}}+\frac{sin^{2}(\varphi-\theta )}{b^{2}}{}} Puis je calcule les portions de surfac...
- 26 Jan 2023, 14:31
- Forum: ✯✎ Supérieur
- Sujet: Croisement d'ellipses
- Réponses: 7
- Vues: 389
Croisement d'ellipses
Bonjour à tous Problème : 2 ellipses égales de même centre, leurs axes font un angle Theta. Aire de la partie commune ? Pour Theta = pi/2 ( ellipses perpendiculaires ) le problème est classique et simple à traiter. En revanche pour theta quelconque , je parviens laborieusement à des sommes d'intégra...
- 25 Jan 2023, 18:47
- Forum: ✯✎ Supérieur
- Sujet: Croisement d'ellipses
- Réponses: 7
- Vues: 389
Re: bornes d'intégrale
En faisant le changement de variable t=ax dans la seconde intégrale, les bornes deviennent : t= a pour x = 1 et t =ab et pour x = b la seconde intégrale devient : \int_{1}^{b}{\frac{dx}{x}}=\int_{a}^{ab}{\frac{a.dt}{a.t}}=\int_{a}^{ab}{\frac{dt}{t}} puis en appliquant la relation de Chasles : \int_{...
- 21 Déc 2022, 12:09
- Forum: ✯✎ Supérieur
- Sujet: bornes d'intégrale
- Réponses: 6
- Vues: 331
Re: bornes d'intégrale
Oui j 'avais oublié que cette relation entre les intégrales est aussi une relation de Chasles.
Bon si je comprends bien, il faut trouver un changement de variable qui modifie les bornes à introduire dans la relation de Chasles ...
Bon si je comprends bien, il faut trouver un changement de variable qui modifie les bornes à introduire dans la relation de Chasles ...
- 20 Déc 2022, 20:31
- Forum: ✯✎ Supérieur
- Sujet: bornes d'intégrale
- Réponses: 6
- Vues: 331
Re: bornes d'intégrale
merci de ta réponse , mais je ne comprends pas bien le rapport entre une somme d'intégrales et une somme vectorielle ( Chasles)...
- 20 Déc 2022, 19:09
- Forum: ✯✎ Supérieur
- Sujet: bornes d'intégrale
- Réponses: 6
- Vues: 331
bornes d'intégrale
Bonjour à tous
Quelqu'un pourrait il m'aider à traiter le problème suivant :
Démontrer sans calculer les intégrales ( cas trivial ) que

avec a et b >0
Quelqu'un pourrait il m'aider à traiter le problème suivant :
Démontrer sans calculer les intégrales ( cas trivial ) que
avec a et b >0
- 20 Déc 2022, 18:09
- Forum: ✯✎ Supérieur
- Sujet: bornes d'intégrale
- Réponses: 6
- Vues: 331
Re: Identité d 'Euler
Je pense que si le produit infini converge uniformément, je peux passer la limite sous le signe produit , mais ça je ne sais pas trop le démontrer...
- 22 Nov 2022, 09:31
- Forum: ✯✎ Supérieur
- Sujet: Identité d 'Euler
- Réponses: 2
- Vues: 479
Identité d 'Euler
Bonjour Voici un exercice (oral X 1986) qui me laisse perplexe. Il s’agissait de démontrer la relation suivante : \frac{sin(t)}{t}=\lim_{p\rightarrow \infty}\prod_{n=1}^{p-1}{(1-\frac{t^{2}}{4p^{2}\tan ^{2}(\frac{n\pi}{2p})}}) Comme indication, il était écrit : démontrer que ...
- 21 Nov 2022, 11:21
- Forum: ✯✎ Supérieur
- Sujet: Identité d 'Euler
- Réponses: 2
- Vues: 479
Re: Somme de série avec intégrales de Wallis
On a donc montré que les deux séries ont la même somme .....
- 12 Nov 2022, 21:57
- Forum: ✯✎ Supérieur
- Sujet: Somme de série avec intégrales de Wallis
- Réponses: 12
- Vues: 985
- 25 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
