Forum de Mathématiques: Maths-Forum

oui bien sûr mon espace E = "suite dont la somme infinie des 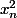converge ...... "
c'est en effet mieux comme ça !!!

En résumé : E espace métrique Si F est dense dans E alors quelque x de E d(x,F) = 0 ton ensemble F = "suite qui s'annule au bout d'un certain rang" est dense dans l'ensemble des suites conclusion si E est l'ensemble de suites, si x est dans E alors d(x,F) = 0 (on définit la distance à l'aide de la n...

Si tu parles de base de Hilbert, ok , mais si tu parles de base au sens usuel, cf wikipedia: http://fr.wikipedia.org/wiki/Base_(alg%C3%A8bre_lin%C3%A9aire) . Concernant la première question, oui en fait cela revient à montrer la propriété suivante: x est dans l'adhérence de F si et seulement si la ...

En effet, j'ai un peu intellectuellement merdouillé ! En fait je voulais savoir si une suite qui tend vers 0 est à une distance nulle de l'espace des suites nulles à partir d'un certain rang... J'ai encore un peu de mal, mais la réponse serait donc oui par un argument de densité ? Sinon pour l'autr...

@ Le-chat Le problème d'une telle base c'est que tu peux avoir un élément qui n'est pas dans l'espace vectoriel : F des suites qui s'annulent au bout d'un certain rang. ex : la suite identiquement égale à 1 est la somme (infinie) de tous les éléments de ta base !! si tu supposes cette base finie, al...

Bonjour, est-ce que si E et F sont deux espaces vectoriels tels que F est dense dans E, alors pour tout vecteur x de F, la distance de x à E vaut 0 ? Autre question : pourriez-vous me donner une base de l'ensemble des suites qui sont nulles à partir d'un certain rang ? Merci :we: Bonjour bizarre ta...

Bonjour fatal error,
c'est noté, j'ai retiré mes liens sur tous mes post !!!

Bonjour,
je poserai :
A = ((1,1,1), (1,j,j²), (1,j²,j)) (désolé je n'y arrive pas en latex ...)
et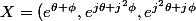
AX = (O1, O2, O3)

après je reconnais que ce n'est pas très clair ton texte ...

Bon je réponds à ma question pour terminer. (c'est la moindre des choses ...)
il suffit de considérer le même calcul que précédemment mais de multiplier par la combinaison 6 parmi 5 ou 6 parmi 1 :

Bonjour,
avec les prérequis suivants : (u²)' = 2uu' et (1/u)' = -u'/u²
tu peux proposer une autre manière de démontrer ....

exactement jlb !!
Mais maintenant une question pour aller plus loin quel est le nombre de possibilités pour 5 noires 1 blanche sans tenir compte de l'ordre ...

Bonjour, j'ai simplement modélisé sous excel et il est vrai que pour les premiers termes cela marche ... mais pour n= 125 on trouve : U(125)= 1842586692361260 = 125 * 14740693538890 (éviter de faire à la calculette ou à la main ....... , mais plutôt à faire au tableur) En espérant t'avoir aidé !!!

Bonjour, bizarre pour un exercice du supérieur ..... mais bon pour le 1) fais un arbre (pas entier pour deux tirages histoire te faire une idée ...) Au premier tirage tu auras 13 manières puis au deuxième encore 13 etc ... imagine le nombre de chemins possibles sur ton arbre En espérant t'avoir un p...

Soit la forme linéaire \varphi:\mathbb{R}\[X\]\mapsto\mathbb{R},\,P\mapsto P(3) . Tu peux trouver une suite (P_n)_n qui converge vers 0 tel que (\varphi(P_n))_n diverge. Merci SaintAmand Ta fonction \varphi (P) est bien une forme linéaire ! oui il semble que ...

SaintAmand a écrit:Bonsoir,



Ça dépend de la topologie choisie pour R[X].

oui en effet, je pense à un espace normé avec la norme suivante pourrait faire l'affaire.

bonjour à tous, je cherche une fonction linéaire non continue 1) il semble que L : R[X]-->R[X] , L(P) = P' n'y soit pas ! ainsi M :R[X]---> R[X], M(P(X)) = X P(X), on a L o M - M o L = Id 2) j'ai montré que L o M^n - M ^n o L = Id aussi pour tout n entier ! voici ma question sur lequel je bloque j'a...

Expérience Expérience de 5 ans dans l'enseignement au collège en tant que professeur certifié d'état. Expérience dans les cours particuliers Titulaire d'une maîtrise de mathématiques Titulaire du BAFA Services Actuellement je me consacre qu'au cours particuliers. Je propose donc mes services dans l...