Forum de Mathématiques: Maths-Forum

Bonjour,

Je bute en vain sur cet exercice que j'ai eu en toute fin de colle sans pouvoir le commencer ( et je n'ai pas eu la réponse ! ) :



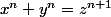
Il nous faut montrer qu'il existe des solutions x,y,z ( on travaille dans N bien sur ).

Merci,

J'avais déja lu tout ça ! Mais sans résultat ! Enfin... si quelqu'un a une idée...

Merci pour la réponse ! Mais je ne vois toujours pas le moyen d'arriver au résultat ! Je ne sais pas dénombrer des partitions en d'autres termes !

Bonjour, j'essaye un exercice tiré d'un site d'un enseignant en CPGE On me donne n \ge 2 J'ai une partie E de [[1,n]] avec n€E et le cardinal de E = q+1 (q € [[0,n-1]] Et je dois donner le nombre de partitions de [[1,n]] contenant E . Je ne vois pas du tout comment procéder ! Merci de l'aide !

Certainement parce qu'il faut enlever la partie A qui contient tous les éléments de E puisque dans ce cas, on ne peut plus définir une partition à deux ensembles ?

Bonjour,

un raisonnement échappe à mon cortex cérébral. Je sais que le nombre de partitions de E en deux ensembles est .

Mais d'où vient ce résultat ?

:we: Merci, l'évidence saute aux yeux maintenant

Bonjour,

j'ai un problème de démonstration pour le cardinal de l'ensemble des injections de E dans F...

Je dois trouver n!/(n-p)! avec p et n les cardinaux de E et F dans le cas où n>p .

Et je ne vois pas comment faire !
Merci pour vos indications.

Bonjour,

j'ai beau cherché, je n'arrive pas à prouver la distributivité de l'intersection sur la différence symétrique !

A savoir que Cn(AB)=(CnA)(CnB)

Double inclusion, retour à la définition, je n'y arrive pas !

Merci pour vos réponses.