26 résultats trouvés
Revenir à la recherche avancée
Le prob c'est que après je tombe sur du :
ln(\frac{1}{1+(\frac{1}{x}))
Et il faudrait montrer que ca tend vers -1.
Comment faire?
- par HH.What?
- 04 Jan 2009, 18:39
-
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une limite
- Réponses: 4
- Vues: 709
Bonsoir, je cherche a calculer une limite en +infini, mais je trouve 2 réponses différentes: f(x) = (\frac{x}{x+1})^(x+\frac{1}{2}) . A la main, je trouve: f(x) = (\frac{1}{1+\frac{1}{x}})^(x+\frac{1}{2}) . D'ou: lim f(x) = (\frac{1}{1+0}&#...
- par HH.What?
- 04 Jan 2009, 18:23
-
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'une limite
- Réponses: 4
- Vues: 709
Soit un repère orthonormé (O, \vec{x}, \vec{y}, \vec{z}) , trouver les deux vecteurs \vec{X} et \vec{Y} tels que : \vec{X}+\vec{Y}=5\vec{x}+3\vec{y}+2\vec{z} \vec{X} ;) \vec{Y}=8\vec{x}-14\vec{y}+\vec{z} (Comment faire le signe produit vectoriel svp?) Mon problème est que je ne sais pas par ...
- par HH.What?
- 14 Sep 2008, 11:47
-
- Forum: ✯✎ Supérieur
- Sujet: Produit vectoriel
- Réponses: 4
- Vues: 806
Pour la 2 je tombe sur: |z-3+2i|=|z+1-i| |z-3+2i|^2=|z+1-i|^2 z=a+ib |a+ib-3+2i|^2=|a+ib+1-i|^2 |a-3+i(b+2)|^2=|a+1+i(b-1)|^2 \sqrt((a-3)^2+(b+2)^2)^2=\sqrt((a+1)^2+(b-1)^2))^2 \sqrt(a^2-6a+9+b^2+4b+4)^2=\sqrt(a^2+2a+1+b...
- par HH.What?
- 14 Sep 2008, 10:57
-
- Forum: ✯✎ Supérieur
- Sujet: Equation second degré
- Réponses: 6
- Vues: 407
Ok, c'est bon ca marche.
Je bloque sur 2 autres, pas évidentes..
(Z-1)=Z^2(Zbarre-1))
(Comment faire le signe barre svp?)
Puis l'autre

- par HH.What?
- 13 Sep 2008, 21:05
-
- Forum: ✯✎ Supérieur
- Sujet: Equation second degré
- Réponses: 6
- Vues: 407
Bonsoir, est-ce que quelqu'un peut me dire où est ma faute svp? car mon résultat ne semble pas correct: z^2+2zcos(\theta)+1=0 Calcul de Delta: \delta=b^2-4ac \delta=4cos^2(\theta)-4 \delta=4(cos^2(\theta)-1) \delta=-4sin^2(\theta) Les racines sont donc : z1=\f...
- par HH.What?
- 13 Sep 2008, 18:59
-
- Forum: ✯✎ Supérieur
- Sujet: Equation second degré
- Réponses: 6
- Vues: 407
Bonsoir, je cherche à savoir comment dériver un vecteur position en physique. Par exemple, si je prend ce schéma, http://img178.imageshack.us/my.php?image=plangt4.jpg Est-ce que l'on pourrait m'expliquer en détail, comment calculer \frac{d\vec{HM}}{d\theta} dans le référentiel (O,x,y). J'aimerais vr...
- par HH.What?
- 09 Sep 2008, 19:32
-
- Forum: ⚛ Physique
- Sujet: Dérivation
- Réponses: 2
- Vues: 564
Bonsoir, je bloque sur la résolution de 2 équations: z^4 = 16e^(\frac{i\pi}{4}) 8(z+1)^6-(z-1)^6=0 Pour la première, j'étais parti sur: z^4 = 16e^(\frac{i\pi}{4}) z^4 = 16(\frac{\sqrt2}{2}+i\frac{\sq2}{2}) z^4 = 8\sqrt2+8i\sqrt2 z^4 = 8\sqrt2(1+i) Mais...
- par HH.What?
- 09 Sep 2008, 17:42
-
- Forum: ✯✎ Supérieur
- Sujet: Nombres Complexes
- Réponses: 2
- Vues: 362
Est-ce que quelqu'un peut me dériver ça une première fois puis une deuxième fois, afin d'obtenir la vitesse et l'accélération dans le système polaires svp?
Parce que je ne sais pas quelle(s) expression(s) s'annule(nt)..
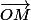
= rcos;)

+ rsin;)
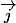
Merci.
- par HH.What?
- 07 Sep 2008, 18:36
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400
Quelle est la différence entre les coordonnées polaires, et le système cartésien?
- par HH.What?
- 07 Sep 2008, 18:28
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400
Et dans ce cas la, pour exprimer
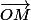
, il faut créer
)
, et dire que:
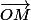
= rcos;)

+ rsin;)
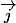
?
(Je parle en polaires..)
- par HH.What?
- 07 Sep 2008, 15:54
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400
Vous parlez d'une base locale?
Créer une base du style (er, e;), ek) ?
- par HH.What?
- 07 Sep 2008, 15:13
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400
Mais par contre, je ne saisis pas quelque chose.
A la base, je devais exprimer une coordonnée en fonction d'un temps
Avec l'équation du cercle la, où puis-je exprimer un temps? :S
- par HH.What?
- 07 Sep 2008, 15:02
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400
Sans développer, j'ai ca:
^2}{r^2} + \frac{(y-y0)^2}{r^2})
,
ce qui est l'équation d'un cercle
^2 + (y-b)^2 = r^2)
- par HH.What?
- 07 Sep 2008, 14:59
-
- Forum: ⚛ Physique
- Sujet: Trajectoire
- Réponses: 13
- Vues: 1400