50 résultats trouvés
Revenir à la recherche avancée
- 30 Sep 2007, 00:41
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
- 29 Sep 2007, 23:34
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
Euh, je ne vois plus très bien ... si \Psi : Im\Phi \rightarrow \mathcal{E} , on a pas \psi^{-1} : \mathcal{E} \rightarrow Im\Phi ? De plus je ne vois pas où j'ai restreint l'espace d'arrivée car il s'agit de \mathcal{E} , qui est l'ev lui même. Désolé j'ai vraiment du mal a visualiser mon erreur !
- 29 Sep 2007, 23:23
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
Hum, en utilisant ce résultat je tombe sur une propriété qui me semble absolument fausse : Je considère \mathcal{E} un \mathbb{K} ev, de dimension infinie. Soit \Phi un endomorphisme injectif de \mathcal{E} . On a Ker\Phi = \{ \mathcal{O} \} . Le théorème du rang s'énonce : Im\Phi est isomorphe à to...
- 29 Sep 2007, 22:01
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
Euh ... j'ai un peu de mal à comprendre ces symboles. Est-ce que cela signifie que 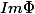 est isomorphe a tout supplémentaire de
est isomorphe a tout supplémentaire de 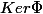 . ?
. ?
- 29 Sep 2007, 21:12
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
Théorème du rang en dimension infinie ?
Bonsoir à tous,
Désolé de poser une question comme ça mais le théorème du rang pourrait-il s'énoncer en dimension infinie ? Et si oui quel en est la bonne version ? (je n'arrive vraiment pas à trouver)
Merci !
Désolé de poser une question comme ça mais le théorème du rang pourrait-il s'énoncer en dimension infinie ? Et si oui quel en est la bonne version ? (je n'arrive vraiment pas à trouver)
Merci !
- 29 Sep 2007, 21:05
- Forum: ✯✎ Supérieur
- Sujet: Théorème du rang en dimension infinie ?
- Réponses: 11
- Vues: 3834
Noter que l'on peut calculer des développements limités en dérivant ... Attention, il n'est possible de deriver que si l'on sait que f' possède un developpement limité d'ordre n-1 au voisinage d'un point a Ainsi f(x)=x^3\sin \frac{1}{x} admet un developpement limité d'ordre 2 au voisinage d...
- 11 Juin 2006, 14:12
- Forum: ✯✎ Supérieur
- Sujet: Produit Scalaire et développement
- Réponses: 2
- Vues: 1502
Salut, bon voila je t'écris pour te raconter un peu mon cas qui ressemble au tien. En terminale, comme la plupart de ceux qui son aujourd'hui en prepa, je ne travaillait que tres peu, comprenant le cours et les exercices sur le moment, et ayant la chance d'avoir une memoire sur le long terme je m'en...
- 13 Fév 2006, 17:16
- Forum: ➳ Orientation
- Sujet: Ai-je le profil ? le niveau ?
- Réponses: 22
- Vues: 4505
- 11 Fév 2006, 21:45
- Forum: ⚔ Défis et énigmes
- Sujet: La mort du bourdon
- Réponses: 12
- Vues: 1877
Qu'est ce que je répondrait ou plutot qu'est-ce que j'ecrairais ? Dans le second cas il n'y aucun doute que j'écrirais "L" "A" "R " "E" "P" "O" "N" "S" "E" ... mais après savoir si j'ai bien répondu :we: Bonne chance a tous
- 04 Fév 2006, 12:56
- Forum: ⚔ Défis et énigmes
- Sujet: Noir
- Réponses: 6
- Vues: 784
- 14 Jan 2006, 20:35
- Forum: ⚔ Défis et énigmes
- Sujet: La mort du bourdon
- Réponses: 12
- Vues: 1877
La mort du bourdon
Bonjour tout le monde, voilà une petite énigme qui m'avait amusé alors je vais vous en faire part. Il y a deux villes: A et B séparées de 1500 km. Un train B part de la ville B vers la ville A à la vitesse de 90 km/h Au même instant, deux évenements se produisent: - Un train A part de la ville A à l...
- 14 Jan 2006, 15:32
- Forum: ⚔ Défis et énigmes
- Sujet: La mort du bourdon
- Réponses: 12
- Vues: 1877
- 12 Jan 2006, 19:35
- Forum: ✯✎ Supérieur
- Sujet: [MPSI] Dévelopement limités
- Réponses: 8
- Vues: 1391
Juste à propos des equivalents, ai je le droit de les passer sous racine: est-ce que 
je sais que l'on ne peut les composer avec des fonctions comme exponentielle mais racine ?
je sais que l'on ne peut les composer avec des fonctions comme exponentielle mais racine ?
- 12 Jan 2006, 19:11
- Forum: ✯✎ Supérieur
- Sujet: [MPSI] Dévelopement limités
- Réponses: 8
- Vues: 1391
- 12 Jan 2006, 18:52
- Forum: ✯✎ Supérieur
- Sujet: [MPSI] Dévelopement limités
- Réponses: 8
- Vues: 1391
[MPSI] Dévelopement limités
Bonsoir à tous! Voilà, j'aimerai savoir s'il est possible de se servir des developement limités dans un calcul de limite. Je n'ai pas encore fait le cour mais le prof nous a donné certaines formules et j'ai plusieurs limites à calculer pour demain. La vraie question est de savoir si l'on peut s'en s...
- 12 Jan 2006, 18:47
- Forum: ✯✎ Supérieur
- Sujet: [MPSI] Dévelopement limités
- Réponses: 8
- Vues: 1391
Problème d'expression ....
Bonjour tout le monde ! Voila j'ai une khôle de français a préparer un texte de francais dans lequel l'auteur parle de "complexe du colonisateur". Voila Si quelqu'un pourrait m'aider a comprendre ce terme je lui en serai infiniment reconnaissant ... P.S: je n'ai rien trouvé sur google et le texte ne...
- 12 Jan 2006, 17:49
- Forum: ♋ Langues et civilisations
- Sujet: Problème d'expression ....
- Réponses: 0
- Vues: 543
attention ... je trouve le point P(0, /3) ... normalement le point (
/3) ... normalement le point ( /3,0) ne te donne pas une fonction impaire dans le nouveau repère ...
/3,0) ne te donne pas une fonction impaire dans le nouveau repère ...
- 08 Jan 2006, 21:34
- Forum: ✎✎ Lycée
- Sujet: Fontions 1èreS
- Réponses: 4
- Vues: 946
- 08 Jan 2006, 21:23
- Forum: ⚔ Défis et énigmes
- Sujet: [Reflexion] Paradoxe du Prisonnier
- Réponses: 48
- Vues: 7453
- 08 Jan 2006, 21:00
- Forum: ⚔ Défis et énigmes
- Sujet: [Reflexion] La fille de madame Dupont
- Réponses: 29
- Vues: 2869
- 50 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
