460 résultats trouvés
Revenir à la recherche avancée
On a dit qu'en 0 il n'y a pas de problème.
Puis en

,
que
 \le e^{-x/2})
qui est intégrable.
Donc I est finie,
C'est une bonne conclusion, non

?
- par rifly01
- 20 Avr 2009, 21:35
-
- Forum: ✯✎ Supérieur
- Sujet: Définition d'ne intégralee
- Réponses: 3
- Vues: 446
Bonjour, Je voudrais montrer que cette intégrale est finie : \displaystyle I = \int_{0}^{+\infty}\exp\left(-x\sin(2x)-\frac{3}{2}x\right)dx Ce que j'ai fait : En 0, On a \sin(2x) = 2x+O(x^2) donc g(x) vaut environ \exp\left(-2x^2-\frac{3}{2}x\right) donc x -->...
- par rifly01
- 20 Avr 2009, 20:55
-
- Forum: ✯✎ Supérieur
- Sujet: Définition d'ne intégralee
- Réponses: 3
- Vues: 446
Bonjour,
J'aimerai connaître les coefficients de ce produit
)
J'ai fait les premiers cas, mais je ne peux pas en déduire une généralisation.
Merci d'avance,
- par rifly01
- 15 Fév 2009, 19:23
-
- Forum: ✯✎ Supérieur
- Sujet: Un produit à expliciter
- Réponses: 2
- Vues: 496
Le premier membre me parait plus correcte.
Pour le deuxième. J'ai vu dans un livre [cf. Jean-Yves Ouvrard] que l'espérance est définie avec
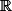
.
Ce sont des sommes. Car je suis dans le discret.
- par rifly01
- 10 Fév 2009, 21:47
-
- Forum: ✯✎ Supérieur
- Sujet: Espérance mathématique
- Réponses: 4
- Vues: 671
Bonjour,
Est-ce que cette cette égalité est juste :
 = \sum_{x\in X(\Omega)}x\mathbb{P}(X=x)=\sum_{x\in\mathbb{R}} x\mathbb{P}(X=x))
Noter la différence : Je somme sur deux ensembles différents
Merci d'avance,
- par rifly01
- 10 Fév 2009, 21:33
-
- Forum: ✯✎ Supérieur
- Sujet: Espérance mathématique
- Réponses: 4
- Vues: 671
Bonjour à tous, Je viens de commencer les probas. Et j'ai quelques problèmes pour calculer la densité du couple (R, \Phi) Enoncé ------- Soit (X_1, X_2) un couple de v.a admettant la densité de probabilité : [CENTER] \displaystyle f(x_1, x_2)=\frac{1}{2\pi(1-b^2)}\tim...
- par rifly01
- 08 Fév 2009, 22:48
-
- Forum: ✯✎ Supérieur
- Sujet: densité de probabilité d'un couple
- Réponses: 1
- Vues: 1447
yos a écrit:On peut écrire f(x,y)=f(x',y'), et en tirer
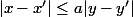
avec le TAF...
Si |a|<1 ça le fait.
Sinon je dirais que ça marche pas.
Merci beaucoup!
- par rifly01
- 10 Jan 2009, 22:58
-
- Forum: ✯✎ Supérieur
- Sujet: Injectivité d'une fonctions
- Réponses: 2
- Vues: 749
Bonjour,
Y a t il une façon simple pour montrer que cette fonction
Soient a et b deux éléments de R,
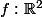
-->

)
-->
, y+a\times sin(x)))
est injective.
La surjectivité m'intéresserait également,
merci,
- par rifly01
- 10 Jan 2009, 22:14
-
- Forum: ✯✎ Supérieur
- Sujet: Injectivité d'une fonctions
- Réponses: 2
- Vues: 749
Merci,
C'est ce que je voulais entendre. Parce que celui qui a fait le livre (d'ou j'ai retiré l'exo) se trompe rarement alors que moi c'est assez souvent. Donc c'est pour cela que je remets en question mon résultat bien que bon.
Merci.
- par rifly01
- 19 Déc 2008, 13:32
-
- Forum: ✯✎ Supérieur
- Sujet: Points critiques
- Réponses: 4
- Vues: 878
Salut,
(1,1) n'est pas solution du système.
(-1/3, 2/3) est une solution du système.
Donc de ce point de vu, j'ai raison. Non ?
- par rifly01
- 19 Déc 2008, 13:22
-
- Forum: ✯✎ Supérieur
- Sujet: Points critiques
- Réponses: 4
- Vues: 878
Bonjour, J'ai une fonction pour laquelle je dois déterminer les extremums et leurs natures. Mon problème c'est que je trouve des points critique qui n'est pas dans la correction. La fonction f(x,y) = y^2-8x^3+4xy Les points critiques que je trouve sont a=(0,0) et b=(1/3, -2/3) Comment j'ai fait : J'...
- par rifly01
- 19 Déc 2008, 12:45
-
- Forum: ✯✎ Supérieur
- Sujet: Points critiques
- Réponses: 4
- Vues: 878
Merci pour votre réponse rapide On est sur des Espaces de Banach. pour une fonction f de deux variables par exemple. f est un isomorphisme au voisinage de (x_0, y_0) ssi J_f(x_0,y_0)\neq 0 En un point pour ne pas vérifier l'injectivité :) Une question naturelle me vient à l'esprit. Q...
- par rifly01
- 10 Déc 2008, 10:31
-
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme
- Réponses: 4
- Vues: 1033
Bonjour à tous,
Comment vérifier qu'une fonction est un isomorphisme. [Une fonction de deux variable ou plus]. ?
Merci d'avance,
- par rifly01
- 10 Déc 2008, 09:53
-
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme
- Réponses: 4
- Vues: 1033
Bonjour, Je cherche à savoir s'il y a équivalence entre : i) La tribu de [0,1] engendrée par {[0, 1/2], [1/2, 1]} ii) La tribu de [0,1] engendrée par {[0,1/2[, {1/2}, ]1/2,0]} Je veux savoir s'il y a cette équivalence pour me ramener à étudier une tribu engendrée par une partition. Merci,
- par rifly01
- 01 Déc 2008, 15:26
-
- Forum: ✯✎ Supérieur
- Sujet: Tribu, tribu engendrée
- Réponses: 1
- Vues: 1401
avec le TAF...