Forum de Mathématiques: Maths-Forum

On pose S= \frac{x^3}{(1+y)(1+z)}+\frac{y^3}{(1+x)(1+z)}+\frac{z^3}{(1+x)(1+y)} . Par symétrie on suppose que x\leq y \leq z . Alors (1+x)(1+y) \leq (1+x)(1+z) \leq (1+y)(1+z) et en appliquant l'inégalité...

j'ai pas fait attention
f est concave sur ]1,+l'infini[

voici ma solution pour ce problème déja sur maths -express
http://www.maths-express.com/bac-exo/congen/olymp05/exo3.php

Bonjour à tous, Soient a,b,c>0 tels que a^2+b^2+c^2=1 Démontrer que \frac{1}{1-ab}+\frac{1}{1-bc}+\frac{1}{1-ca} \leq \frac92 Bonne chance! on a la fonction x----> \frac{1}{1-x} est concave sur IR+ alors \frac{1}{1-ab}+\frac{1}{1-bc}+\frac{1}{1-ca} \leq \frac{9}{3-(ab+bc+ac)} d'autre par ab...

pour 1)
on a

pour la convergence de An
ona sigma(1/n^2) converge (série de rieman alors An converge

Bonjour,je bloque sur cet exercice dont voici l'énoncé ABC est un triangle 1-Construis E puisque: vecCA+2vecCE=vec0 J'ai besoin d'une figure pour que je comprenne Merci d'avance bonjour, si vecCA+vecCE= vec0, c'est que vecCA=-vecCE=vecEC les vecteurs CA et EC ont un point commun, les points A, C et...

lui il n'as pas parlé de système il a dis equation à deux inconnus :hum:

pour résoudre une equation à deux inconnu on ecrit un des inconnu en fonction de l'autre
pour cette equation
3x-y=9
-y=9-3x
y=3x-9
donc les solutions sont S={(x , 3x-9) / }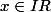
je crois que tu as compris la démarche :id:

megrabi a écrit:J'ai cherché des questions d'olympiad francaise, me je n'ai trouvé rien. Vous voulez me dire ou je peut trouver ca ?

Merci

aller aux
http://www.animath.fr

f est une fonction liniaire telle que lorsque X=-8 alors f(x) =4.8 1: déterminer le fonction ( x) (donner les 2écriture de f) 2: quel est son coeficient? 3: calculer f(3) puis f(racine de 2) 4: calculer X si f(x) =3 5: tracer la représentation graphique de cette fonction f( juste vu que vou pouvez ...

les conditions sur x et y ????

:we: c'est ce qu'on appelle l'esprit mathématique :id:
(NB t'as oublié une condition donnée dans l'enoncé origine xyz>=1)

on a



donc

Samir

de la meme manière tu poses a=(x+y) et b=(x-y) alors 2x=a+b et 2y=a-b d'ou la relation à démontrer devient 2sin(a) sin (b) = cos(a+b) -cos (a-b) d'autres part on a cos(a+b)=cosacosb-sinasinb (1) cos(a-b)=cosacosb+sinasinb (2) (2)-(1)donne cos (a-b) -cos(a+b)=2sin(a) sin(b) et c'est la relation deman...

tu poses a=(x+y) et b=(x-y) alors 2x=a+b et 2y=a-b d'ou la relation à démontrer devient 2cos (a) sin (b) = sin (a+b) -sin (a-b) d'autres part on a sin(a+b)=sinacosb+sinbcosa (1) sin(a-b)=sinacosb-sinbcosa (2) (1)-(2)donne sin (a+b) -sin (a-b)=2cos (a) sin (b) et c'est la relation demandée :we:

Mikou a écrit:le grand mathador ne connait pas la méthode de cardan ? c'est un scoop :happy3:

:hein:
voici un lien qui explique cette methode

http://fr.wikipedia.org/wiki/Formules_de_Cardan

ona \frac{1+ab}{1+a}+\frac{1+bc}{1+b}+\frac{1+ac}{1+c} =\frac{1+ab}{a(1+bc)}+\frac{1+bc}{b(1+ac)}+\frac{1+ac}{c(1+ab)} on pose x=\frac{1+ab}{1+bc} y=\frac{1+bc}{1+ac} z=\frac{1+ac}{1+ab} (xyz=1) donc \frac{1+ab}{1+a}+\frac{1+bc}{1+b}+\frac{1+ac}{1+c} =\frac{x}{a}+\frac{y}{b}+...

salut
Montre que
toute matrice symétrique positive est le produit d'une matrice triangulaire par sa transposée