4 résultats trouvés
Revenir à la recherche avancée
Re: Densité des polynômes D --> D dans H(D,D)
En utilisant l'inégalité triangulaire/ continuité de la norme comme argument peut être ...
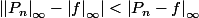
- 24 Jan 2022, 02:48
- Forum: ✯✎ Supérieur
- Sujet: Densité des polynômes D --> D dans H(D,D)
- Réponses: 5
- Vues: 585
Re: Sphere complexe
Bonsoir, l'équivalent complexe "parfait" en 3D du plan complexe n'existe pas mais par contre ce qui est utilisé pour représenter des points sur un espace 3D sont les quaternion qui sont en 4D, l'intérêt étant de définir les rotations comme la multiplication avec un quaternion unitaire . Le...
- 24 Jan 2022, 02:38
- Forum: ✯✎ Supérieur
- Sujet: Sphere complexe
- Réponses: 6
- Vues: 761
Re: Borne Sup et Inf
Bonsoir, Je suppose qu'il faut montrer que l'inf de A appartient à l'adhérence de A ce qui se montre en utilisant la définition séquentielle de l'inf d'une partie et ensuite tu montre qu'il n'appartient pas à l'intérieur de A par l'absurde (en supposant que l'inf de A \in l'intérieur de A et en mont...
- 22 Jan 2022, 02:54
- Forum: ✯✎ Supérieur
- Sujet: Borne Sup et Inf
- Réponses: 1
- Vues: 310
Re: Densité des polynômes D --> D dans H(D,D)
Bonsoir, Il me semble qu'il y a une erreur au tout début de la démo, ce n'est pas parce que f est holomorphe qu'elle est développable en série de taylor (elle n'est dérivable qu'une seule fois). je te conseille aussi de regarder la définition séquentielle de la densité, car si f était développable e...
- 22 Jan 2022, 02:43
- Forum: ✯✎ Supérieur
- Sujet: Densité des polynômes D --> D dans H(D,D)
- Réponses: 5
- Vues: 585
- 4 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
