Exact,Aspx s'est trompé,c'est bien 17/2.
Ciao et bonne continuation!
83 résultats trouvés
Revenir à la recherche avancée
- 26 Avr 2006, 16:37
- Forum: ✎✎ Lycée
- Sujet: Problème de calcul
- Réponses: 6
- Vues: 783
Géométrie dans l'espace
Tu es bien parti:le point d'intersection M de (QR) et (EF) appartient à la face (EFGH) [puisqu'il appartient à (EF)] et au plan (RQS) [puisqu'il appartient à (QR)].Le point S aussi appartient à (EFGH) et (RQS).Donc l'intersection de (RQS) avec la face (EFGH) est la droite (MS) [ou plutôt la partie d...
- 26 Avr 2006, 12:08
- Forum: ✎✎ Lycée
- Sujet: geometrie dans l'espace
- Réponses: 1
- Vues: 798
Géométrie
Le 1/ est juste:x=2-V3.
Sinon on écrit "hypoténuse" sans h derrière le t.
Pour le 2/,je crois qu'il y a une erreur dans l'énoncé,je trouve k=2-hV3 et non le contraire.Mais tu as posé les bonnes équations et inéquations.Tu es donc sur la bonne voie.
Ciao et bonne continuation!
Sinon on écrit "hypoténuse" sans h derrière le t.
Pour le 2/,je crois qu'il y a une erreur dans l'énoncé,je trouve k=2-hV3 et non le contraire.Mais tu as posé les bonnes équations et inéquations.Tu es donc sur la bonne voie.
Ciao et bonne continuation!
Problèmes de plans
Il s'agit d'un exercice d'optimisation. La zone en question représente le polyèdre des contraintes (des contraintes économiques qu'on aurait dû te présenter au début de l'exercice,elles correspondent aux 3 équations de plans du début). 12x+13y+10z=t est l'équation d'un plan P(t). Tous les plans P(t)...
- 22 Avr 2006, 17:34
- Forum: ✎✎ Lycée
- Sujet: Petit probleme plans :)
- Réponses: 1
- Vues: 700
Produit scalaire
Désolé,mais c'est illisible!
- 22 Avr 2006, 17:14
- Forum: ✎✎ Lycée
- Sujet: les produits scalaires
- Réponses: 4
- Vues: 943
Salut à toi! Même si j'ignore complètement le sens du verbe "dibber",au 1/ il suffit de redonner les chiffres initiaux et après une année(pas franchement compliqué!). Pour le 2/,révise les suites arithmétiques(c'est-à-dire de la forme u(n+1)=u(n)+r) En fait u(n)=u(0)+nr=u(1)+(n-1)r=....=u(p)+(n-p)r ...
3ème degré
Mais ma parole qu'est-ce qu'on vous apprend à l'école? A l'époque,c'était plus tard ces équations-là! Bon si tu as une équation du type ax^3+bx^2+cx+d=0,tu dois te ramener à une équation du type x^3+px+q=0(trouve un moyen de te débarrasser du x^2,par exemple en mettant sous forme canonique(ax^3+bx^2...
- 09 Fév 2006, 13:07
- Forum: ✎✎ Lycée
- Sujet: Equation du troisième degré :
- Réponses: 8
- Vues: 2069
Système matriciel
Il semblerait que c'est un cas général.La solution est unique si ta matrice est inversible(de déterminant non nul). Utilise la méthode du pivot de Gauss. Si par exemple,tu as un système à 3 équations et 3 inconnues x,y,z,alors il faut se ramener à 3 équations:une contenant les 3 inconnues,puis une a...
- 09 Fév 2006, 12:47
- Forum: ✎✎ Lycée
- Sujet: Résoudre système matriciel
- Réponses: 1
- Vues: 482
Tétraèdre
Ce tétraèdre est un peu comme un repère orthogonal. OA=ai OB=bj OC=ck M est sur le plan (ABC) s'il existe deux réels k et l tels que AM=kAB+lAC. Alors A est le barycentre de (M,1),(B,-k),(C,-l). (x-a,y,z)=k(-1,1,0)+l(-1,0,1) Donc x=-k-l+a y=k z= l u(-1,1,0) et v(-1,0,1) sont deux vecteurs directeurs...
Enoncé?
Il me semble que ça fait zéro! J'ai dû me planter quelque part? En tout cas tes primitives sont bonnes à une constante près. N'oublie pas qu'une fonction admettant une primitive en admet une infinité,car c'est à une constante près.Donc on ne dit pas "LA primitive de f",mais "UNE primitive de f". Ciao!
- 30 Jan 2006, 18:44
- Forum: ✎✎ Lycée
- Sujet: probleme primitive
- Réponses: 5
- Vues: 836
Lapin compris?
ParLaLaSortie a écrit:2- Sialors
avec
donc
.
Bonjour!
Excuse-moi,mais je n'ai pas compris l'immédiateté de
Peux-tu m'expliquer davantage?
Merci d'avance.
Ciao!
- 28 Jan 2006, 16:52
- Forum: ✯✎ Supérieur
- Sujet: Tribu trace
- Réponses: 6
- Vues: 2144
Bonjour!
Excuse-moi,mais je n'ai pas compris l'immédiateté du 2/.Pourrais-tu expliquer davantage.
Merci d'avance.
Ciao!
Excuse-moi,mais je n'ai pas compris l'immédiateté du 2/.Pourrais-tu expliquer davantage.
Merci d'avance.
Ciao!
- 28 Jan 2006, 16:45
- Forum: ✯✎ Supérieur
- Sujet: Tribu trace
- Réponses: 6
- Vues: 2144
Lapin compris?
Bonjour!
Excuse-moi,mais je n'ai pas compris l'immédiateté du 2/.Pourrais-tu expliquer davantage.
Merci d'avance.
Ciao!
Excuse-moi,mais je n'ai pas compris l'immédiateté du 2/.Pourrais-tu expliquer davantage.
Merci d'avance.
Ciao!
- 28 Jan 2006, 16:42
- Forum: ✯✎ Supérieur
- Sujet: Tribu trace
- Réponses: 6
- Vues: 2144
Quoi!?
Combien vaut a?
Tribu trace
Bonjour! J'ai un gros problème avec un exercice sur les tribus. Soit A la tribu sur l'ensemble E engendrée par une classe B de parties de E. Soit A' l'ensemble des intersections de F inclus dans E avec les éléments de A. Montrer que A' est la tribu sur F engendrée par les intersections de F avec les...
- 27 Jan 2006, 18:37
- Forum: ✯✎ Supérieur
- Sujet: Tribu trace
- Réponses: 6
- Vues: 2144
Suites,suite et fin
Pour ultime information,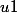 =5 et
=5 et  =4 ,donc
=4 ,donc 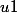 -
- =1.
=1.
- 25 Jan 2006, 17:51
- Forum: ✎✎ Lycée
- Sujet: Exo de TS sur les suites
- Réponses: 4
- Vues: 635
Suites,suite
3/ $u_{n+1}-v_{n+1}$ <1/2( $u_{n}-v_{n}$ ) Donc $u_{n}-v_{n}$ <1/2( $u_{n-1}-v_{n-1}$ ) Par conséquent, $u_{n+1}-v_{n+1}$ <1/2*1/2( $u_{n-1}-v_{n-1}$ ). Tu peux ainsi remonter jusqu'à zéro,en multipliant chaque fois par 1/2. Ce qui te donnera fatalement une puissance de 1/2. Je te rappelle au passag...
- 25 Jan 2006, 13:00
- Forum: ✎✎ Lycée
- Sujet: Exo de TS sur les suites
- Réponses: 4
- Vues: 635
Suites
Salut! 1/ $u_{n+1}$ - $v_{n+1}$ =( $u_n$ + $v_n$ )/2- $sqrt(u_nv_n)$ =.5( $sqrt(u_n)$ - $sqrt(v_n)$ )^2 Il fallait quand même voir l'identité remarquable! Ceci étant positif, $u_{n+1}$ > $v_{n+1}$ pour tout n. 2/ $sqrt(a)$ - $sqrt(b)$ < $sqrt(a)$ + $sq...
- 24 Jan 2006, 18:27
- Forum: ✎✎ Lycée
- Sujet: Exo de TS sur les suites
- Réponses: 4
- Vues: 635
Proportions
En fait c'est le coefficient de proportion a qui te donnera la part de chacun.
Le premier touchera a*2*5*3/810
Le second touchera a*5*12*4/720
Le dernier touchera a*1*20*9/900
La somme de tout ça donne 7700.
Tu en déduis a.
Tu conclus pour chacun.
cqfd
Ciao!
Le premier touchera a*2*5*3/810
Le second touchera a*5*12*4/720
Le dernier touchera a*1*20*9/900
La somme de tout ça donne 7700.
Tu en déduis a.
Tu conclus pour chacun.
cqfd
Ciao!
- 18 Jan 2006, 20:05
- Forum: ✎✎ Lycée
- Sujet: problème de proportions
- Réponses: 4
- Vues: 968
Trigo
Pour N,ce n'est pas 4,mais 2!
Pour le reste,je suis dans un cyber et n'ai pas de papier sous la main pour calculer,désolé.
Pour le reste,je suis dans un cyber et n'ai pas de papier sous la main pour calculer,désolé.
- 16 Jan 2006, 18:19
- Forum: ✎✎ Lycée
- Sujet: svp pouvez vous m'aider pour un pb de trigo?
- Réponses: 7
- Vues: 1280
- 83 résultats trouvés - Page 1 sur 5 • 1, 2, 3, 4, 5
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
