42 résultats trouvés
Revenir à la recherche avancée
Salut. Je bloque sur la 1c). En appliquant la propriété fondamentale à G, j'arrive à 8MG=9MA-MC (MG, MA et MC étant des vecteurs). Mais je ne vois pas comment élever MA et MC au carré. Tu peux penser au produit scalaire et plus précisemment au carré scalaire : MA^2=\vec{MA}^2=\vec{MA} \cdot \vec{MA}
- 26 Avr 2008, 20:06
- Forum: ✎✎ Lycée
- Sujet: Croissant de lune (lieux géométriques)
- Réponses: 2
- Vues: 1375
Bonjour.
Déjà, qu'as tu trouvé pour cette question ?
Ashleyy a écrit: Par quelle transformation C est-il l'image de M ?
Déjà, qu'as tu trouvé pour cette question ?
- 20 Avr 2008, 13:00
- Forum: ✎✎ Lycée
- Sujet: Homothéties
- Réponses: 2
- Vues: 707
Bonjour. Je pense que la question 2a) c'est du cours ............. Pour la 2b), il faudra remplacer ton y par 2 et ton x par 3 dans l'équation que tu auras trouvé à la question 2a). Ceci te donnera une équation dont l'inconnue est a............. Pour la 2c) il te suffiras de remplacer les valeurs de...
- 20 Avr 2008, 12:40
- Forum: ✎✎ Lycée
- Sujet: résolution sur un exercice de dérivation
- Réponses: 3
- Vues: 694
youngforever a écrit:Pour la question suivante, comme on sait que G isobarycentre de A,B,C et D, il faut trouver les coordonnés des dits points afin de trouver ceux de G en utilisant la propriété des barycentres.
Ok t'es sur la bonne voie,
- 13 Avr 2008, 19:04
- Forum: ✎✎ Lycée
- Sujet: melange, barycentres, produits scalairs et limites
- Réponses: 12
- Vues: 1405
ax^2/-x donne une forme indéterminée. lim x->-oo Qu'est-ce que tu racontes là !!! Je te signale que \frac{ax^2}{-x}=-ax ......et la limite de ça en -\infty tu sais faire. On lève donc cette forme indé en faisant: pour tout réel x différent de 0: ax^2/-x = x(ax/-1) et -oo/-1=+oo Puisque x tend vers ...
- 13 Avr 2008, 18:57
- Forum: ✎✎ Lycée
- Sujet: [1ere S] exercice de maths: Etudes de fonctions
- Réponses: 10
- Vues: 1453
- 13 Avr 2008, 18:49
- Forum: ✎✎ Lycée
- Sujet: melange, barycentres, produits scalairs et limites
- Réponses: 12
- Vues: 1405
L'énoncé te dit que le point M : -- est sur le segment [AB] ; -- ses coordonnées dans le repère (B;\vec{BA},\vec{BI}) sont (x,0) ; -- est distinct du point F . Quelles sont les coordonnées (dans le repère (B;\vec{BA},\vec{BI}) ) des points A, B et F ? Avec ça et compte-tenu d...
- 13 Avr 2008, 18:31
- Forum: ✎✎ Lycée
- Sujet: melange, barycentres, produits scalairs et limites
- Réponses: 12
- Vues: 1405
Bonsoir. * Pour les question 1a) et 1b) c'est bon. *Pour la question 1c) ...... vu que x \in [0,+\infty[ , quel est le signe du dénominateur de f_{1}^{'}(x) ? Et celui du numérateur ? Tu peux alors conclure que f_{1}^{'}(x) est ..... sur [0,+\infty[ et donc que f_...
- 13 Avr 2008, 18:16
- Forum: ✎✎ Lycée
- Sujet: exercice analyse TS
- Réponses: 23
- Vues: 9117
Salut. La première question tu sais faire jpense ? On te demande juste de prouver que (pour x \in ]2,+\infty[ ) on a : \frac{x+1}{x+2}=1+\frac{3}{x-2} .... ce que tu peux faires dès la quatrième ! Pour la deuxième question, tu te donnes un x \in ]2,+\infty[ et t'éssaies de comparer f(x) avec...
- 13 Avr 2008, 17:06
- Forum: ✎✎ Lycée
- Sujet: "CrOisSaNcE d'uNe FonCtIOn"
- Réponses: 11
- Vues: 1304
Alors, pour faire la limite de f(x), cela revient à faire la limite de ax² puisqu'il s'agit du plus haut coefficient. Euhhhhhhh, ce n'est pas ça. Calculer la limite de f(x) en -\infty par exemple revient à calculer la limite en -\infty du quotient des termes de plus haut degré (puisqu'ici t...
- 13 Avr 2008, 15:53
- Forum: ✎✎ Lycée
- Sujet: [1ere S] exercice de maths: Etudes de fonctions
- Réponses: 10
- Vues: 1453
youngforever a écrit:Il ne me semble pas qu'il manque une lettre !
A mon avis, le point
Sinon, qu'as tu trouvé pour la question a) ?
- 13 Avr 2008, 15:33
- Forum: ✎✎ Lycée
- Sujet: melange, barycentres, produits scalairs et limites
- Réponses: 12
- Vues: 1405
Bonjour.
Commence par rectifier ton énoncé !!! Il manque une lettre !?
Tu bloques où ? As-tu fais une figure ?
youngforever a écrit: F le point de [AB] tel que F= 3/4AB( vecteur)
Commence par rectifier ton énoncé !!! Il manque une lettre !?
youngforever a écrit:Je bloque complétement, est ce que quelqu'un pourrais m'aider s'il vous plait
Tu bloques où ? As-tu fais une figure ?
- 13 Avr 2008, 15:13
- Forum: ✎✎ Lycée
- Sujet: melange, barycentres, produits scalairs et limites
- Réponses: 12
- Vues: 1405
Bonjour.
D'après que ton cours, pour un entier , que vaut :
, que vaut :  ?
?
lolotte43 a écrit:J'arrive pas à trouver la limite en fait... :S
D'après que ton cours, pour un entier
- 13 Avr 2008, 15:06
- Forum: ✎✎ Lycée
- Sujet: Petit problème sur mon DM... [Term ES]
- Réponses: 4
- Vues: 812
Bon déjà on obtient  , ce qui te fournit :
, ce qui te fournit :
 .
.
Essaie de faire de même pour trouver en fonction de
en fonction de  et
et  .
.
Après ça, selon toi, à quoi les conditions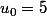 et
et 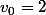 te serviront ?
te serviront ?
Essaie de faire de même pour trouver
Après ça, selon toi, à quoi les conditions
- 13 Avr 2008, 14:49
- Forum: ✎✎ Lycée
- Sujet: Les suites 1ere STL
- Réponses: 4
- Vues: 941
Ben alors, c'est que 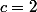 et donc ce résultat te fournit la réponse et la justification pour la première question.
et donc ce résultat te fournit la réponse et la justification pour la première question.
Allez, on passe à la deuxième question .....
Allez, on passe à la deuxième question .....
- 13 Avr 2008, 14:37
- Forum: ✎✎ Lycée
- Sujet: [1ere S] exercice de maths: Etudes de fonctions
- Réponses: 10
- Vues: 1453
Bonjour. Voici quelques indications sous forme de questions qui te permettront de mener à bien ton exercice. 1) En regardant l'expression de f(x) , que vaut f(0) ? En regardant ton tableau de variations, que vaut f(0) ? 2) En regardant l'expression de f(x) , que vaut ...
- 13 Avr 2008, 14:22
- Forum: ✎✎ Lycée
- Sujet: [1ere S] exercice de maths: Etudes de fonctions
- Réponses: 10
- Vues: 1453
Bonjour.
N'y a t-il pas une erreur dans ton énoncé ?
Je pense plutôt que décroit sur
décroit sur 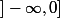 de
de  à
à  !???
!???
Skartak a écrit:f(x) décroissant sur ]-infini;0] en -infini et 2
N'y a t-il pas une erreur dans ton énoncé ?
Je pense plutôt que
- 13 Avr 2008, 14:08
- Forum: ✎✎ Lycée
- Sujet: [1ere S] exercice de maths: Etudes de fonctions
- Réponses: 10
- Vues: 1453
- 13 Avr 2008, 13:54
- Forum: ✎✎ Lycée
- Sujet: Les suites 1ere STL
- Réponses: 4
- Vues: 941
Bonjour. Ton énoncé n'est pas très explicite, mais bon je pense qu'on te demande de déterminer les coordonnées des points d'intersection de la parabole (\mathcal{C}) d'équation y=x^2-3 avec la droite (\Delta) d'équation y=x+3 . Détermines d'abord les solutions de l'équation x^2-3=x+3...
- 13 Avr 2008, 00:46
- Forum: ✎✎ Lycée
- Sujet: Résolution Algébrique
- Réponses: 3
- Vues: 660
- 12 Avr 2008, 23:43
- Forum: ✎✎ Lycée
- Sujet: Equadiff [TS]
- Réponses: 33
- Vues: 2585
- 42 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
