Forum de Mathématiques: Maths-Forum

En passant respectivement par les bases 2, 3, 4, 9, (mais pas 10) ça doit coller :zen: Qu'appelles-tu un critère de divisibilité par un nombre ? Quelle est ta situation initiale (ta donnée) ? Je parle des critères de divisibilité usuels, à savoir : 2 : un nombre est divisible par 2 lorsque le chiff...

Ce sont des critères très simples. Pour au moins la divisibilité par 2, tu n'as pas d'idée ? Admettons pour 2 : Tout nombre a peut sécrire : a=10b+a0 où a0 appartient à {0;2;4;6;8}. 10b est divisible par 2 donc a0 doit l'être aussi. L'écriture 10b+a0 est quand même très fortement inspirée de la déc...

Bonjour, Je suis un peu perdue sur la propriété de la borne supérieure ( toute partie non vide admet une borne supérieure). Sur un site je trouve ça : Définition. R est défini comme devant satisfaire aux conditions suivantes : (i) R est un corps totalement ordonné, (ii) R est une extension de Q, (ii...

Bonjour,

J'aimerais savoir s'il est possible de démontrer les critères de divisibilité (par2,3,4,9) sans passer par la décomposition en base 10 ?

Merci

Mathusalem a écrit:

C'est ça le propos de Manny (y = x^2 et y = x^3 -2). Un seul point de coupure, mais pas tangent.

:hein:

Où est la tangente ici ?

Manny06 a écrit:une parallèle à l'axe coupe la parbole en un point unique mais ce n'est pas une tangente

Je ne considère que les droites qui sont des courbes représentatives de fonctions.

Bonjour, J'ai une question sur la notion de tangente. La tangente à une courbe en un point est vue depuis la 1éres comme la droite passant par un point et ayant comme coefficient directeur le nombre dérivé de la fonction en ce point. Pour les cercles la définition de la tangente est la droite qui co...

XENSECP a écrit:Bah sachant que j'ai jamais entendu parler du deuxième je me pose même pas la question !

Trouve sur wikipédia

wikipédia ne donne pas de réponse satisfaisante.

XENSECP a écrit:Connait pas taux de variation

Je serais tentée de dire que c'est la même chose que le taux d'accroissement d'une fonction... mais pourquoi deux noms différents alors.

Bonjour,

J'aimerais savoir quelle est la différence entre ces deux définitions mathématiques:
-taux d'accroissement;
-taux de variation.

Merci :zen:

Bonsoir, On a les différentes variables aléatoires suivantes : -variable aléatoire réelle; -variable aléatoire réelle discrète; -variable aléatoire réelle continue; -variable aléatoire continue à densité; J'aimerai avoir des exemples de variables aléatoires réelles mais ni discrète ni à densité et d...

Ta question de départ était de savoir si on pouvait définir la pente d'une droite verticale. Je réponds que c'est une pente de valeur infinie, par déduction de l'équation d'une droite. Il est vrai que "valeur infinie" est en soi une sémantique un peu curieuse, on ne peut pas "valoris...

nodjim a écrit:Le coefficient directeur pour les droites est défini, c'est l'infini.

Et dans quel ouvrage avez-vous trouvée cette définition ?

Tu as tout à fait raison, mais les Mathématiques se doivent d'être cohérentes. La pente infinie résulte simplement de l'équation de la droite. On ne peut donc pas mettre la droite verticale à part. Mais ça présuppose que le coefficient directeur est défini pour les droites verticales. S'il est défi...

y est une ordonnée, elle ne peut être égale à infini, tout au plus peut-on la faire tendre vers l'infini. Et on a alors une forme indéterminée du type Infini/infini. En tous les cas, ça ne me choque pas de dire qu'une droite verticale possède une pente infinie, je l'ai déjà entendu dire par des pro...

Les droites y=a(x-P) passent toutes par le point y=0 et x=P non ? et ce quelle que soit la valeur de a. Si j'ai bien compris votre raisonnement : On part d'une droite d'équation y=ax+b. On fixe un point P qui est le point d'intersection de cette droite avec d'axe des abscisses. Notons y=a'x+b' l'éq...

C'est, à y bien réfléchir, une question bien embarrassante... Soit y=ax+b la droite et on veut trouver toutes les droites qui pivotent autour d'un pivot P situé sur l'axe des x. yP=0 donc P=-b/a et donc b=-aP Ces droites se réécrivent alors: y=ax-aP et donc x=(y+aP)/a=y/a+P Donc si a est infini, y/...

Je suis entièrement d'accord avec vous, j'ai surement posté cette question dans la mauvaise partie du forum : ce n'est pas la définition à donner à des lycéens qui m’intéresse mais sa définition exacte. C'est à dire est-ce qu'il faut parler de coefficient directeur égal à + infini ou de non existenc...

Bonjour,

Je m'interroge sur la définition exacte du coefficient directeur d'une droite.
Est-il défini seulement pour les droites non verticales ou est-il égal à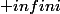 pour ces droites.

Merci

Le 'i' est bien le 'i' des complexes.

J'ai développé les exponentielles, j'ai essayé d'utiliser les formules trigonométriques mais mon problème au dénumérateur reste entier.

Hummm je me suis trompée de a, a=1/r+b+n.