Forum de Mathématiques: Maths-Forum

Salut achille :)

Est-ce qu'il faut utiliser le lemme de Gronwall ?

Merci à vous :)

Désolé pour le retard !

Oui je cherche donc une solution de la forme

Salut

Je cherche à résoudre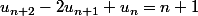

Donc l'équation homogène est :



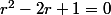
Donc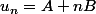 avec A et B réels.

Maintenant comment poursuivre pour trouver la solution générale ?

merci

Salut

J'ai un doute !

On considère deux suites

Si on a en l'infini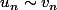

A-t-on alors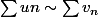

Je dirai non puisuqu'on ne peut pas sommer des équivalents mais bon j'ai un doute !

Merci

Salut :)

Il faudrait peut-être nous dire en quoi tu cherches la limite :lol:

Sinon, un bon moyen est d'utiliser la quantité conjuguée :)

DOnc utilise plutôt l'autre formule de Cauchy ici (celle de base pour un ouvert convexe) :

C'est bizarre sur le cercle |z|=2 ta fonction est holomorphe !

Donc l'intégrale vaut 0 non ?

Pose

Alors

Or est holomorphe en dehors de donc d'après la formule de Cauchy :

Salut :)

Tu connais le calcul des résidus ?

Salut :)

Change de logiciel dans ce cas :lol:

Sur maple, cette primitive s'exprime en fonction que de deux ou trois log

oui fahr :)

Pas d'idée ?

ok :)

On te demandais : Trouver la quantité d'apareils pour 250euros

IL faut donc résoudre 0,2 (x + 20) (x-50)=0

Tu la résout et tu trouves x=50 car x=-20 est impossible.

Voilà c'est fini :)

Salut oscar :)

Oui mais je voulais le faire chercher un peu !

Salut

Déterminer une primitive de :



Bon courage

(avec la méthode, pour éviter d'utiliser Maple :ptdr: )

La résolution de l'équation avec le discriminant te donne deux solutions ici.

Ensuite, grâce à ton cours, tu en déduis une factorisation de ton polynôme, celle que je t'ai donné :)

Non !

L'équation est :

Soit en passant 250 de l'autre côté, on a :

Tu te trompes, le discrimant vaut 196

Avec ma solution : un produit de facteurs est nul ssi l'un au moins des facteurs est nul.

Ensuite tu verras qu'une des solutions ne peut pas convenir.

Si tu ne sais pas le faire, remarque que :