Forum de Mathématiques: Maths-Forum

Bon vraiment je ne vois pas, pourtant ça a l'air simple je suis peut-être trop débile pour le voir, je vais passer cette question ce sera mieux.

Merci en tout cas pour ta réponse Decrey, passe une bonne fin de journée !

D'accord merci ! Donc normalement le devrait apparaître tout seul ?

Bonjour, j'ai un exercice où je me retrouve bloqué dès la première question et je viens quérir un peu de votre aide pour avancer. L'énoncé : Soit (u_n)_{n\in\mathbb{N}} une suite strictement positive telle que \lim\limits_{n \rightarrow +\infty} \frac{u_{n+1}}{u_n}=l avec 0\leq l<1 . 1. Mont...

Tournesol merci beaucoup pour ton com je regarde ça ce soir

Mais bon même en sachant ça je ne vois pas trop à quoi ça m'avance
En tout cas merci à vous trois pour votre aide, bonne soirée

My bad c'est bon j'ai trouvé d'où il sort

J'aimerais juste savoir comment Ben314 fait pour conclure à l'aide de la première équation que f(x/2)=f(x)/4 quelque soit x L'égalité (1) donne f(x)=f(r(2)x)/2 On remplace x par x/r(2) f(x/r(2))=f(x)/2 puis on applique cette dernière égalité : f(x/2)=f(x/r(2))/2=f(x)/4 Remarque r(2) = racine de 2 J...

J'aimerais juste savoir comment Ben314 fait pour conclure à l'aide de la première équation que f(x/2)=f(x)/4 quelque soit x

tournesol a écrit:La résolution de la deuxième donne : f(x)=g(x) +x^2 , avec g continue et 1 périodique .
Autre piste ?

Non merci c'est gentil j'aimerais trouver par moi-même, de plus ton indice ne m'aide pas vraiment ^^'

mathelot a écrit:C'est simple,tous les résultats que tu trouves doit être vérifiés par la fonction carré.

Oui la ou les fonctions trouvées doivent vérifier les deux équations, mais j'imagine que vous avez eu le réflexe de le voir de suite, or le réflexe de mon côté je ne l'ai pas

Comment tu arrives à conclure ça pour la première ? Que f(x/2)=f(x)/4 ?

Pour f(0)=8 j'ai pris la seconde équation et remplacé x par 0, ce qui donne avec f(1)=5
Et f(1) je l'ai trouvé en cherchant plusieurs expressions avec f(1) et f(-1) dedans

Effectivement, mais alors du coup ça veut dire que je me suis trompée dans mes calculs ?
Si à un moment je trouve f(a)=b mais qu'au final ça ne vérifie qu'une équation sur les deux.. ?

Bonjour bonjour, j'ai un système d'équations fonctionnelles à résoudre et je coince : Trouver toutes les fonctions continues de f:\mathbb{R}\rightarrow\mathbb{R} vérifiant \begin{cases} f(\sqrt{2}x)&=2f(x)\\f(x+1)&=f(x)+2x+1 \end{cases} À un moment j'arrive à ...

Ce n'est pas un résultat de cours ... ce n'est pas un argument que tu peux réutiliser, c'est juste un petit sujet d'exercice si ça t'amuse, et c'est surtout un truc qui peut t'aider à sentir les résultats. Du coup tu es en train de dire que en gros si la fonction est croissante et convexe à chaque ...

D'accord, merci beaucoup pour ton aide en tout cas !

Attends attends... Comme elle est positive sur donc la suite est croissante ?

Tout le temps positive (my bad).

Oupsi pardon, je ne referai plus l'erreur :facepalm:.

Négative en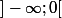 et positive en 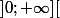? Pourquoi ?

La suite récurrente (u_n)_{n \in \mathbb{N}} est croissante et majorée par 0, alors elle tend vers son unique point fixe l=0 . Pas OK car tu n'as pas montré que la suite est croissante (voir mon exemple de la fonction racine carrée). Il faut étudier le signe de u_{n+1}-u_n . Du coup ça revi...