Forum de Mathématiques: Maths-Forum

bien essayé mais ça n'as pas pris... les mines approchent, avec le stress, quant aux vacances faut pas y compter avant quelques mois!

bonjour
commence par faire un dessin et cherche un triangle rectangle dans la figure
tu pourra apliquer pythagore

bonjour
utilise les questions precedentes en remarquant que les 3 egalités sont liées entre elles

bonjour
commence par faire un schéma et dis nous sur quoi tu bloque

nan la derniere egalité est fausse c'est CB*HA/4 sinon ca n'a pas de sens (2*2 = 4 et pas 1^^)

bonjour
BCD est isocele rectangle donc l'angle BDC vaut 90/2 = 45°
ADE vaut donc 180 - 60 - 45

oué je me suis gourré remplace le D par un B dans tt mes messages^^

mmh nn tu as aire de NHC = HC*NI /2 = CI * HA/2 or CI = CD/2 tu remplace et tu reconnais l'aire de ADC/2

autre chose
ce ne serait pas RS = racine( 9^2 +9^2) = racine(81 +81) et non 92 + 92 ?
je ne sais pas si c'est une erreur de frappe ou que j'ai mal compris

pour que la distance CH soit la plus courte il faut que (CH) soit perpendiculaire a (RS) donc on a (CH) perpendiculaire a RH donc le triangle RCH est rectangle en H il s'inscrit donc dans un cercle dont RC est l'un des diametre (theoreme que tu as du voire en cours je suppose ) d'ou la reponse a la ...

tu peut donc en tirer NI * CH en fonction de CI et AH

mmh tu fais une erreur dans le theoreme c'est CN/AC et non AN/AC
et CI/CH et non HI/HC

bonjour
je me trompe peut etre mais si tu ecrit q = ordre de 5 alors


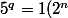ca doit pouvoir marcher comme ca nn ?

bonjour
pour la a)
on sait que le point h est quelquepart entre R et S donc
xr < xh < xs
donc -4 < xh < 5
donc 0 < xh +4 < 9
donc 0 < (xh+4)/9 < 1 donc il existe k entre 0 et 1 tel que k = (xh+4)/9
d'ou xh = 9k-4
voila pour xh
fait pareil pour yh

bonjour
commence par faire un schéma
ensuite tu écrit : NHC = (NI * CH) /2 et ABC = (AH * DC) /2

avec le théorème de thales appliqué aux triangles semblables CIN et CHA tu trouve NI * CH et tu tomberas très vite sur le résultat

bonjour, non je ne vais pas me moquer de toi, moi aussi j'ai eu du mal au début, perso, je le retiens comme ca: si w = xt alors comme x est une constante par rapport à t (x ne s'écrit pas f(t) ), on a dw / dt ( = dérivée de w par rapport à t) = x donc w = x dt je ne sait pas si c'est ça que tu deman...

tu n'a pas besoin des points d'intersection de f et y
maintenant que tu as l'equation b avec comme solution x1 et x2 il te suffit de calculer f(x1) et f(x2) pour avoir les coordonnées demandées dans c)

<< 2) On cherche à déterminer les points de Cf en lesuals la tangente à Cf est parallele à la droite (D) d'équation y= 9x+4

il faut que les pentes soient égales
il faut donc que les dérivées soient égales
donc f'(x) = y'(x)
et tu as ton équation

Si tu fais x^3 -3x² +2 = 9x+4 c'est comme si tu cherchais les intersections entre y et Cf
Ce n'est donc pas le bon raisonnement il me semble

la pente de la tangente en un point x c'est la dérivée de f en ce point