Forum de Mathématiques: Maths-Forum

Merci pour les réponses,

Ce que j'ai compris en gros est que cette discussion a pour but de lever l'indétermination des valeurs "chaudes" de x (de la forme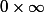 ici), c'est bien ça ?

Merci beaucoup pour l'explication mais j'ai peur qu'il n'y ait un petit malentendu =x. La question est peut être plus simple que cela. Je sais que certaines notations de séries doivent vérifier quelques conditions pour avoir un sens, mais je parle plutôt de suites de fonctions (au sens propre). par ...

Bonjour, Je débute en séries de fonctions et j'aimerais avoir un petit éclaircissement sur un point que je comprends pas tout à fait (concernant déjà les suites de fonctions). En étudiant la convergence simple de quelques suites de fonctions il arrive très souvent que l'on discute la convergence en ...

Bien compris, merci !

Bonjour, Alors on me propose de montrer que si M dans Mn (IK) alors il existe P dans IK[X] tel que M^(-1) = P(M). Comme indication il faut remarquer que la famille (Id,A,...,A^n²) est liée, je ne sais pas à quoi correspond A, je l'ai supposée dans Mn(IK). En tout cas j'ai pu montrer sans difficulté ...

Bonjour à tous, Je veux montrer que E= C([0,1],IR) muni de la norme infinie, est un Banach. Une première étape (imposée par l'exo) est de montrer que toute suite f_n de Cauchy de E converge dans IR. On a donc à partir d'un certain rang : sup_{x \in [0,1]} |f_n (x) - f_p (x)| \leq \ep...

Ah pardon, j'avais mal compris.

Maintenant je comprends bien mieux, merci beaucoup.

Evidemment, mais a est supposé dans IQ* non pas dans IZ.

Bonjour à tous, On me demande de justifier l'inexistence d'un a dans IQ* tel que IQ = a IZ. J'ai commencé par supposer son existence afin de trouver une contradiction. Ce n'est pas possible de supposer l'existence d'une bijection puisque c'est l'objet de la question suivante. Une indication svp ? In...

En effet, merci bien :)

Bonsoir à tous, Bizarrement je n'arrive pas à démontrer cette inégalité : (1+t)^x \ge 1 + t^x Avec t réel strictement positif, et x \in [1,\infty[ Ce serait évident avec x entier, car ici, je ne peux aborder formule du binôme généralisée (supposée non acquise). Une indication svp ? Merci de ...

Bah.. C'est ce que j'ai fait, en développant le produit seuls les termes "semblables" restent car la base est orthonormée.

C'est au niveau du gradient que je bloque, en tout cas j'ai l'impression qu'il y a un truc qui ne tourne pas rond, ma tête peut être :dodo:

D'abord merci pour ta réponse, Alors j'ai posé Xp,Yp,Zp les coordonnées de \vec {P} dans mon repère cartésien, Xr,Yr,Zr celles de \vec {r}. Le produit scalaire donne XpXr+ YpYr+ZpZr. Mais comment y appliquer le gradient ? j'ai dans mon cours l'expression analytique en cartésien (celle avec les dériv...

Bonjour à tous, Ce n'est qu'aujourd'hui qu'on a vu une brève idée sur le gradient (définition et composantes dans les divers systèmes de coordonnées). Et c'est là que je bloque dès la première question, que je trouve parachutée =x On me demande de calculer le gradient du produit scalaire \vec{P} . \...

D'accord, je me doutais que cela soit complètement rigoureux.

Merci tize :)

Bonsoir, En naviguant sur la toile je suis tombé par hasard sur un exemple anecdotique de la complexité des CAPTCHA (codes à saisir dans les sites web pour différencier les bots des humains, bref peu importe, j'ai décidé de m'y mettre), celui là demande la résolution d'une équation, assez enflée de ...

Oui bien sûr, et c'est bon j'ai trouvé, merci pour tout :)

Bonsoir,

Le problème c'est que mon système est composé de trois équations identiques, à coefficient près, donc je ne peux pas en tirer grand chose..

Merci bien nonam.

Je pourrais me débrouiller avec cette méthode, toutefois je suis obligé de maitriser la méthode du sev engendré car la question suivante me l'impose (la même pour F= {v de IR^3, f(v)= -3v}, de dim 1.. )

Je suis d'accord, mais on doit quand même montrer qu'elle est linéaire non ?