27 résultats trouvés
Revenir à la recherche avancée
Ok donc je fais : X(w)=\int x(t) e^{-jwt} dt mais comme x(t) est paire alors x(t)=x(-t) et donc X(w) = \int x(-t) e^{-jwt} dt et donc avec le changement de variable y=-t : X(w) = -\int x(y) e^{-jw(-y)} du = -\int x(y) e^{-j(-w)y...
- 05 Nov 2009, 10:09
- Forum: ✯✎ Supérieur
- Sujet: Propriétés transformée fourier
- Réponses: 5
- Vues: 709
Merci, juste une derniere question, à cette ligne ) = \frac{1}{a} \int x(u) e^{\frac{w}{a}u} du = \frac{1}{a}X( \frac{w}{a})) , sachant que
, sachant que
F{x(t)} = X(w), comment sait-on que e^{\frac{w}{a}u} du = X( \frac{w}{a})) ?
?
F{x(t)} = X(w), comment sait-on que
- 05 Nov 2009, 08:00
- Forum: ✯✎ Supérieur
- Sujet: Contraction transformée de fourier
- Réponses: 5
- Vues: 1435
Merci pour la réponse, mais de quelle changement de variable parles tu? de t à y avec y=-t ou de x(t) à y avec y=-x(t), et dans le dernier cas ca ne m'a pas l'air d'un changement de variable vu que x n'est pas une variable?
- 05 Nov 2009, 07:55
- Forum: ✯✎ Supérieur
- Sujet: Propriétés transformée fourier
- Réponses: 5
- Vues: 709
Propriétés transformée fourier
Bonjour, J'étudie en ce moment les transformées de fourier et il a certaines propriétés que je ne comprends pas : 1) si x(t) est réelle et paire, alors X(w) est réelle est paire 2) si x(t) est réelle et impaire, alors X(w) est imaginaire pure et impaire Si vous connaissez les démonstrations de ces d...
- 05 Nov 2009, 06:12
- Forum: ✯✎ Supérieur
- Sujet: Propriétés transformée fourier
- Réponses: 5
- Vues: 709
Merci pour la réponse, Pour la deuxieme ligne \int x(at)e^{wt} dt , ca devrait pas plutot etre \int x(at)e^{jwt} dt . Aussi, pourquoi ne pas mettre at au lieu de seulement t au niveau de la puissance de l'exponentielle, de sorte à avoir \int x(at)e^{jwat} dt . Aussi, je n'ai ...
- 05 Nov 2009, 06:09
- Forum: ✯✎ Supérieur
- Sujet: Contraction transformée de fourier
- Réponses: 5
- Vues: 1435
Contraction transformée de fourier
Bonsoir,
Quelqu'un pourrait me donner une piste pour démontrer la transformée de fourier après contraction du domaine, c'est a dire :
F{ x(kt) } = 1/k X(w/k)
Merci d'avance
Quelqu'un pourrait me donner une piste pour démontrer la transformée de fourier après contraction du domaine, c'est a dire :
F{ x(kt) } = 1/k X(w/k)
Merci d'avance
- 04 Nov 2009, 18:19
- Forum: ✯✎ Supérieur
- Sujet: Contraction transformée de fourier
- Réponses: 5
- Vues: 1435
Je connais mon cours et je sais que c'est une équation differentielle linéaire. Mais pour cette forme, je peux utiliser cette technique avec le facteur d'integration qui est x dans ce cas(en enlevant la valeur absolue). Donc je multiplie les deux cotés de l'equation par le facteur d'integration et j...
- 23 Juin 2009, 17:20
- Forum: ✯✎ Supérieur
- Sujet: Equation differentielle
- Réponses: 2
- Vues: 571
Merci pour la réponse, pour ce qui est de la constante devant l'exponentiel, je ne vois pas de quoi tu parles.A propos de la valeur absolue, il faut donc séparer les valeurs de x en deux intervalles: x<0 et x>0, c'est bien ca? Sinon en général il est vrai que la variable indépendante dans les équati...
- 23 Juin 2009, 13:47
- Forum: ✯✎ Supérieur
- Sujet: Equation differentielle
- Réponses: 2
- Vues: 571
Equation differentielle
Bonjour, Je souhaite résoudre l'équation différentielle linéaire : \frac {dy} {dx} + \frac {1} {x} y = \exp (x) Donc pour ce la je calcule le facteur d'integration(je crois ke ca sapelle comme ca) qui est : e^{\int \frac 1 x \, dx} = e^{ln |x| + C } = |x| Pour ce qui est de la constante d'in...
- 23 Juin 2009, 07:28
- Forum: ✯✎ Supérieur
- Sujet: Equation differentielle
- Réponses: 2
- Vues: 571
C'est bizarre, cette équation différentielle n'est pas linéaire il me semble?!
J'ai une racine de y, c'est pas de la forme d'une équation linéaire normalement?
J'ai une racine de y, c'est pas de la forme d'une équation linéaire normalement?
- 11 Juin 2009, 14:23
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
et la tu developpe t'aura Y=t^4 + 2Ct + C^2 et la: en faisant l'ddition de Y et y_0 ça donnera f(t) = y_0 + c' +t^4 + 2Ct + C^2 et tu posera k = C²+C' . comme ça dans la solution general tu n'as que K. fin c'est une façon de parler mais il y aura le 2Ct (tu le supprime pas non plus ) De plus j'ai p...
- 11 Juin 2009, 14:13
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Merci pour la réponse mais je ne comprend pas pourquoi il ne devrait pas y avoir de condition pour le C avant d'élever au carré.A cette ligne, la ligne 2, \sqrt y = t + C, C \in \Re alors qu'à ce niveau il est clair que t + C doit etre positif et donc que si on choisit un C qui fait que t+C est néga...
- 11 Juin 2009, 14:08
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Je fais le cas 1 :
si y > 0 alors:
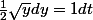

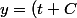^2)
Normalement j'arrive à là mais le truc c'est que je ne vois pas ce qu'il en est à propos de la constante C quand je suis à la ligne 2.
si y > 0 alors:
Normalement j'arrive à là mais le truc c'est que je ne vois pas ce qu'il en est à propos de la constante C quand je suis à la ligne 2.
- 11 Juin 2009, 12:33
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Merci pour la réponse donc ca se passe comment?
si C est inférieur à -t² alors C + t² est négatif est dans ce cas racine(y) devrait l'etre aussi selon l'égalité ce qui n'est pas possible donc je ne vois comment faire.
si C est inférieur à -t² alors C + t² est négatif est dans ce cas racine(y) devrait l'etre aussi selon l'égalité ce qui n'est pas possible donc je ne vois comment faire.
- 11 Juin 2009, 12:27
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
- 11 Juin 2009, 12:04
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Merci pour la réponse mais j'ai déja fais cette étape(dsl je ne l'ai pas précisé). Le problème est après l'integration ou je me retrouve avec une racine de y ou une racine de -y et je voudrais savoir est ce que ca pose des conditions pour la constante d'integration et pour t et si oui lesquels. pour...
- 11 Juin 2009, 11:44
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Exercice équation différentielle
Bonjour, J'ai un exercice sur les équations différentielles que je n'arrive pas à résoudre à cause d'une valeur absolue qui me pose problème. Sois l'équation différentielle dy/dt = 2*racine(abs(y)). Je montre tout d'abord que la fonction y(t) = 0 est solution de l'équation. Puis on me demande de tro...
- 11 Juin 2009, 08:11
- Forum: ✯✎ Supérieur
- Sujet: Exercice équation différentielle
- Réponses: 13
- Vues: 1369
Merci pour la réponse mais j'ai pas trop compris ce que ça veut dire,à ce que j'ai compris a distribution binomiale c'est lorsque qu'on fait une expérience aléatoire plusieurs fois sachant qu'il y a deux issues possibles, dans ce cas ce serait quoi cette expérience et les deux issues possibles?
- 26 Jan 2009, 16:33
- Forum: ✯✎ Supérieur
- Sujet: Exercice de proba
- Réponses: 4
- Vues: 816
Exercice de proba
Bonsoir, J'ai un exercice de probabilité sur lequel je bloque,je cite l'énoncé: Soit une société qui doit envoyer N lettres à N destinataires.Chaque lettre correspond à un destinataire particulier parmi les N destinataires. Cette société envoie les N lettres au hasard. On définit une variable aléato...
- 26 Jan 2009, 01:14
- Forum: ✯✎ Supérieur
- Sujet: Exercice de proba
- Réponses: 4
- Vues: 816
- 04 Aoû 2008, 20:25
- Forum: ✯✎ Supérieur
- Sujet: Recherche fonction bijective
- Réponses: 10
- Vues: 2165
- 27 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
