Forum de Mathématiques: Maths-Forum

merci stef !

La découverte implique la médaille Fields et pas le contraire! Tous les mathématiciens qui ont fait une découverte majeure ont le niveau d'une médaille Fields (avec une majuscule s'il te plaît!) Un doctorat n'est pas un niveau d'études "astronomique" et c'est effectivement à partir de ce ...

Merci !

Pour enrichir un peu le débat :

quelqu'un peut-il me citer une découverte majeure et "récente" en mathématiques...(disons des 50 dernieres annees)

Merci à vous !

tu peux faire une recherche sur l'ouvrage de référence de Poisson:

"Recherches sur la probabilité des jugements"

@+

De rien,

Tu abordes un sujet intéressant mais malheureusement pas suffisament traité sur le forum..

@+

Il y a quelques problèmes sur le formulaire, il y a des fois où tu transformes pas la formule. Et de plus, \int_a^b f(t)^{dt} ne veut strictement rien dire :lol: C'est une notation inventé de toute pièce et de plus ca n'est pas cette notation que j'ai employé ! en gros c'est le produit des ...

Resalut,

historiquement j'ai trouvé ca:

http://www.math93.com/theoreme/notions_mathematiques.html

puis tu cherche "Loi de Poisson" dans la page

a confirmer

A+

tu peux obtenir la loi de poisson comme limite de la loi binomiale pour n très grand et p suffisament petit ...il y a des demonstration de ca

Oui arithmétique, merci,

Au fait, tu as lu le formulaire, en particulier les méthodes d'interpolation, ca me semble plus précis que les methodes classiques pour des modèles du type de a*Exp(bx) ou 1/(ax+b)...

merci à toi,

Bonjour à tous, Voila, je me suis amusé à transformer des formules à base d'addition en formules à base de produits: Ainsi: on transforme donc une addition: a + b en produit: a * b on transforme une soustraction: a - b en division: a / b on transforme un produit: a*n en puissance: a ^ n on transform...

Merci beaucoup pour votre exposé !

Je me permet de vous envoyer un message privé ou je vous précise mon problème.

Merci encore.

J'en suis bien conscient

Je souhaite simplement ramener cette expression à un nombre "complexe"...

genre:


)

Bonjour à tous ! Pourriez-vous m'aider à simplifier cette formule: (-2)^{0.25} \ (-3)^{0.2} \ (-4)^{3.2} puis-je écrire (-1)^{(0.25 + 0.2 + 3.2)} \ (2)^{0.25} \ (3)^{0.2} \ (4)^{3.2} = (-1)^{3.65} \ (2)^{0.25} \ (3&#...

ReSalut, Tu pars d'abord de : 1/k >= \int_k^{k+1} dt/t\ en applicant la somme de 1 a n à gauche et a droite du signe, on a \sum_{k=1}^{n} 1/k >= \sum_{k=1}^{n} \int_k^{k+1} dt/t\ et avec : \int_1^{n+1} dt/t\ = ln(n+1) tu devrais obtenir: H(n) >= ln(n+1) ----------------------...

Pour b :

Tu pars de sur l'axe des abscisse et tu te déplace vers la gauche de jusqu'a point ou la tangente en à la courbe de coupe l'axe .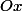

Tu as donc la pente de la tangente

@ +

Bonsoir, Tu imagine par exemple une courbe croissante sur R+ et qui coupe l'axe des Ox. Si tu considère le point A(a,0) ou la courbe de f coupe l'axe des abscisses. Tu pars de x_n situé a droite de a et tu considère alors la tangente en x_n a la courbe de f. Cette tangente de pente f'...

Combien de fois faudra-t-il que j'écrive que l'on ne donne pas la réponse aux exercices mais qu'on aide l'élève à la trouver lui-même!

Veux-tu montrer à tout le monde que tu sais faire? Ou bien ne comprends-tu pas une consigne pourtant simple à priori!

Pour la modération

cos(x+pi)=-cos(x)

désolé de t'avoir orienté sur une fausse piste,

tu fais comme l'a dit Babe:

tu calcul

Un+1 - Un

si
(Un+1 - Un)>0 alors elle est croissante
(Un+1 - Un)<0 elle est décroissante..

@+

Tu calcule la dérivée, tu regarde pour quel valeur de n la dérivée s'annule (extremums) et ensuite tu etudie le signe (positif=croissant, negatif=decroissant) entre les extremums...

tu as fait les derivées ?