150 résultats trouvés
Revenir à la recherche avancée
Ben314 a écrit: Attention quand même au fait que, si x n'est pas proche de a, de "pousser le D.L plus loin", ça ne marche pas toujours...
Par exemple, le D.L. de ln(1+x), aussi loin qu'on le calcule ne donnera jamais d'approximation de ln(3)=ln(1+2)...
Merci en effet pour les précisions ^^
- par Edward
- 07 Avr 2010, 10:35
-
- Forum: ✯✎ Supérieur
- Sujet: Formule de Taylor-Young
- Réponses: 17
- Vues: 2379
Ta formule est vrai pour tout x. Cependant, au voisinage de 0 le petit tau de x^4 va faire que tu peux "confondre" exponentielle avec la partie polynomiale du DL. Cette approximation sera d'autant plus précise que tu pousse ton DL loin ou que tu te rapproches de 0.
- par Edward
- 07 Avr 2010, 10:16
-
- Forum: ✯✎ Supérieur
- Sujet: Formule de Taylor-Young
- Réponses: 17
- Vues: 2379
Pour la question 2 il faut appliquer le théorème des valeurs intermédiaires. En quelle classe es tu exactement ?
- par Edward
- 07 Avr 2010, 10:08
-
- Forum: ✎✎ Lycée
- Sujet: algo dichotomie
- Réponses: 3
- Vues: 981
Un algo par dichotomie consiste à diviser à chaque étape la longueur ton intervalle de recherche de ta racine par 2. La racine se trouve sur ton intervalle [a,b]. Donc soit (a>0 et b<0) ou soit (a<0 et b>0). Prend c le milieu du segment [a,b]. Tu doit pouvoir te ramener à un intervalle deux fois moi...
- par Edward
- 07 Avr 2010, 09:48
-
- Forum: ✎✎ Lycée
- Sujet: algo dichotomie
- Réponses: 3
- Vues: 981
Je suppose que je devrais répondre convergente mais je vois pas trop pour quoi ...
- par Edward
- 04 Oct 2009, 13:45
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
Comme DA je trouve
)=-\frac{1}{2n^2}+o\left(\frac{1}{n^2}\right))
.
Si j'ai bien compris je dois trouver un grand tau d'une suite dont la somme partielle converge, c'est ça ?
- par Edward
- 04 Oct 2009, 12:16
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
Je ne vois pas comment ça m'aide à conclure. Comment je repasse à ma série une fois le DA établi ?
- par Edward
- 04 Oct 2009, 11:47
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
Un exercice sur les séries : je doit trouver la nature de la série de terme général ln ( cos (1 / n ) ). Si on écrit l'expression de la some partielle on peut utiliser la formule ln(a) + ln(b) = ln(a*b), et on se retrouve avec ln du produit que je cherche. En fait il suffirait de montrer que le prod...
- par Edward
- 04 Oct 2009, 11:40
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
J'oublie toujours le 2 dans la formule...
Sinon oui je suis sur que c'est cos(1/k).
- par Edward
- 04 Oct 2009, 11:14
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
Bonjour,
J'ai un petit : je n'arrive pas à calculer : produit de k = 1 à n des cosinus (1/k). J'ai essayé 2,3 trucs (utiliser la formule sin(2x) = sinx cosx par exemple) mais je n'arrive à rien... je dois louper quelque chose.
Quelqu'un pourrait-il m'aider ?
- par Edward
- 04 Oct 2009, 11:07
-
- Forum: ✯✎ Supérieur
- Sujet: Formule cosinus
- Réponses: 15
- Vues: 1399
Je pense qu'on s'est mal compris sur le tableau de signe, je m'explique :

Donc par exemple, sur l'intervalle ]-infini;-3], h est positive, sur [-3;-1], négative, ainsi de suite.
- par Edward
- 13 Sep 2009, 09:10
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188
Non ce n'es pas ça (regarde bien les - et les + sont alternés), en fait je t'ai déjà factorisé h(x) totalement, tu n'a plus qu'à faire la tableau ! Je te conseille te t'entraîner sur cette formule de factorisation, histoire que tu chope le coup.
- par Edward
- 13 Sep 2009, 09:01
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188
Attention
(x^2-1)=(x-3)(x+3)(x-1)(x+1))
D'après la formule (en fait tu dois applique la formule à chacun des facteurs). Ça devrait aller mieux pour le tableau ^^.
- par Edward
- 13 Sep 2009, 08:55
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188
Euh tu voulais surement dire ligne ^^.
Dans ta première ligne tu marque les bornes de l'intervalle et les valeurs d'annulation, après tu met autant de lignes qu'il y a de facteurs dans ton produit, puis enfin dans la dernière ligne tu met ta fonction.
- par Edward
- 13 Sep 2009, 08:46
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188
Euh je vois pas trop ce que tu veux dire... l'idée est que pour un facteur, si on a répertorié sa ou ses valeurs d'annulation, il restera de signe constant entre ces valeurs. Comme tu peux le voir dans le tableau, il faut que tu rentre dans ta première ligne les bornes de l'intervalle (ici l'infini ...
- par Edward
- 13 Sep 2009, 08:36
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188
Pour factoriser h , utilise la formule
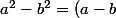(a+b))
.
Pour le tableau de signe je te fais un scan où il y aura un exemple, laisse moi 2 min ^^
EDIT : voila

- par Edward
- 13 Sep 2009, 08:29
-
- Forum: ✎✎ Lycée
- Sujet: equation du second degrès
- Réponses: 41
- Vues: 3188


