Forum de Mathématiques: Maths-Forum

est-ce que tu aurais une idée pour un découpge de cette figure:

pour pouvoir faire des calcul simple comme la figure précédément?

En faite j'ai travailler avec les coordonnées des points d'intersections et je trouve la bon résultat. Par contre comment prouver que l'on a bien un triangle equilateral??? (sans utiliser les coordonnees de point) Et oui le resultat c'est bien celui que tu as trouver Par contre comment fait tu pour ...

j'ai reussi a trouver la solution, par contre j'ai un petit problème:


Comment montrer que l'aire des arcs rouges sont tous égales aux arcs vert???

bonjour, J'ai cette figure avec un carré de coté 1, http://hpics.li/b37b564 Je doit calculer l'aire totale de la fleur c'est a dire ce ce qu'il y a en bleu + "les pétales qui joignent les sommets" J'ai calculer les pétales et je trouve a la fin l'air qui vaut: \pi - 2 maintenant il faut qu...

Des indication s'il vous plait pour la question 4????

OK
Quelqu'un peut m'aider juste pour la question 2:

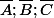
2. Montrer que seules les combinaisons {A;B;C} et {} peuvent être composées d'événements non indépendants deux à deux.

Comment je fais?

Pour la 1)a une combinaison est complète si les probabilités de ses événements permettent de reconstituer les trois probabilités élémentaires : P(A) , P(B) et P(C) j'ai fais: p({A,B})=p(A)*p(B) et p(C)=p(A)(C|A)+p(B)(C|B) donc {A,B,C} est complete. p{ \bar{A},\bar{B} } = 1-p(A)+1-P(B)=2-(p(A)+P(B))=...

Bonjour Soient 3 éléments élémentaires A,B et C. 1) Une combinaison d'événements autres que \emptyset et \bar{\emptyset} est dite complète si la donnée des probabilités de chacun de ses événements induit la probabilité de tous les événements. En d'autres termes, la combinaison C est complète si deux...

c'est bon ce que j'ai fais?????

Pour la 2)b) je doit montrer que: \forall n \in IN, \sigma_N(f)(\theta)-f(\theta)=\dfrac{1}{2\pi} \int_{\phi = 0}^{2\pi} (f(\theta-\phi)-f(\theta))F_N (\phi) d\phi d'apres 2)a) \forall n \in IN, \sigma_N(f)(\theta)=\dfrac{1}{2\p...

Pour le 2)a) je doit montrer que \forall n \in IN, \sigma_N(f)(\theta)=\dfrac{1}{2\pi} \int_{\phi = 0}^{2\pi} f(\phi) F_N (\theta-\phi) d\phi = \dfrac{1}{2\pi} \int_{\phi = 0}^{2\pi} f(\theta-\phi)F_N (\phi) d\phi Sachant que: \sigma_N(f)(\...

on sait que sin(\frac{\theta}{2})> sin(\frac{\delta}{2}) car sin(x) est croissant entre 0 et \dfrac{\pi}{2} et sin(\frac{\delta}{2})> sin(\frac{\theta}{2}) car sin(x) est décroissant entre \dfrac{\pi}{2} et \pi \forall n \in IN, \\ F_N( \theta)=\dfrac{1}{N+1}\...

L3

mais il n'y a rien d'autre au dénominateur, il y a que sa

\forall n \in IN, \forall \delta \in ]0,pi[, \forall \theta tel que \delta< \theta<2\pi-\delta \\ F_N(\theta)=\dfrac{1}{N+1}\dfrac{sin^2(\dfrac{(N+1) \theta}{2})}{sin^2(\dfrac{\theta}{2})} \\ \delta< \theta<2\pi-\delta \\\\ \dfrac{\delta}{2}<\dfrac{\theta}{2}<\dfrac{...

Pour la d)

Comment je montre

pour le 1)c)
j'arrive pas à intégré
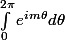
pour m different de 0 je doit trouver 0

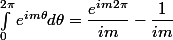
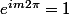
Pourquoi c'est p-etre tt bete mais je voit pas

c'est bon pour le 1)b) j'ai compris Maintenant pour le 1)c) Je trouve \forall n \in IN,\frac{1}{2\pi} \int_{\theta = 0}^{2\pi} F_N (\theta) d\theta = \frac{1}{2\pi} \int_{\theta = 0}^{2\pi} \frac{1}{N+1}\frac{sin^2(\frac{(n+1) \theta}{2})}{sin^2(\frac{\theta}{2})} d\t...

\sum_{n} D_n = \frac{1}{sin(\theta/2)} \sum_{k=0}^n Im (e^{i \theta/2} e^{i k \theta}) = \frac{1}{sin(\theta/2)} Im( e^{i (n+1)\theta/2}\times \frac{sin((n+1)\theta/2)}{sin(\theta/2)}) Pourquoi?? Moi je trouve: \sum_{k=0}^n Im (e^{...

Rectification d'énoncé c'est bien

Pourquoi tu met alors que l'enoncé nous dit