Forum de Mathématiques: Maths-Forum

Bonjour, Ok pour le domaine de définition. Ensuite c'est une simple application du théoreme du cours qui parle d'échange de limite/série de fonction. Si on appelle 3$ f_n(x)=\fr{1}{n^x} . Grâce à la convergence uniforme des fn sur les intervalles [a,+inf[ a>1, et parce qu'ils admettent une l...

Bonjour, 8$ \star Hum, tu as du faire une erreur dans la détermination du sous espace propre associé à la valeur propre 1. 3$ E_{1}=ker(A-I_3)=\{(x,y,z)\in\mathbb{R}^3 \ | \ \left{{ y+z=0 \\ x+y-z=0\}= \{(x,y,z)\in\mathbb{R}^3 \ | \ \left{{ x=2z \\ y=-z \}=vect{\left( \ 2...

De rien :)

Salut ! Dans la méthode générale pour résoudre des ED linéaire du 2nd ordre à coefficients constants, on procede comme ceci : 1) On résoud l'équation différentiel sans second membre. Ceci nous donne une fonction dépendant de 2 parametres, nommons la 3$ y_0 . Dans ton cas, 3$ y_0(t)=A\exp(...

L'application 3$ y_1(t)=t-\fr{3}{2} ne satisfait pas (E1) : 3$ y_1^{"}(t)-2{y_1}^'(t)+y_1(t)=0-2\times 1 + t - \fr{3}{2}= t -2 - 3/2 = t + 7/2 \neq t+1/2 Pose 3$ y_1(t)=at+b , calcul y1' et y1'', ensuite détermine a et b pour que y1 soit solution de (...

Bonjour :) Tu peux commencer par linéariser le cosh ce qui t'ammene à trouver une solution particuliere de 3$ (E) : \ y^{"}-2y'+y=x+\fr{1}{2} + \fr{1}{2}\cosh(2x) Ensuite il te suffit d'utiliser le théoreme de superposition: Si f est solution de 3$ (E1) : \ y^{"...

Tout simplement avec les équations qui définissent ton domaine et principalement le cercle, ou sinon avec un peu de géométrie : Regarde le triangle OBM ou B(2,0) et ou M est un point se promène sur le cercle. Ce triangle est rectangle en M car le triangle est inscrit dans le cercle et que l'un de ce...

Bonjour, Dis moi si je me trompe mais ton Domaine de départ est bien D_1=\{(x,y)\in\mathbb{R} / \ x^2+y^2-2x\leq 0, \ y\geq 0 \} (soit le demi cercle supérieur de centre (1,0) et de rayon 1 ) ? Si c'est bien ça, alors pose le changement en polaire x=rcos(t), y=rsin(t). Ainsi ton nouveau doma...

Si on prend y_p(x) =\fr{1}{3}\exp{\fr{5}{2}x} , alors \rm 2y_p^'(x) - 5y_p(x) = \fr{5}{3}\exp{\fr{5}{2}x}-\fr{5}{3}\exp{\fr{5}{2}x} = 0 \neq 2\exp{\fr{5}{2}x} non ? Donc yp(x)=1/3exp(5x/2) n'est pas solution de ton equation. Pose yp(x) = (ax+b)exp(5x/2) avec a,b dans R et...

Bonjour, Ton équation différentielle est linéaire et à coefficients constants, et aux vues de la forme du second membre elle suggère une solution particulière de la forme yp(x) = Q(x)exp(5x/2) ou Q est un polynôme de degré inférieur ou égale à 1. Pose yp comme dit plus haut et identifie les coeffici...

Bonjour,
Il suffit de trouver une solution particuliere à l'équation différentielle.
Vous pouvez chercher dans les applications du type vu que le second membre est un polynôme.

Bonsoir,

Pour le 1ere exo,
Tu pars de ta fonction .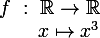
Tu as donc et . Comment montrer que deux membres sont égaux ?
As-tu développé le membre de droite de ton égalité ?

Bonjour à tous ! Posons f: \mathbb{R} \to \mathbb{R} \\ x \mapsto sin(4\pi x). . Pour te rentre compte de l'indétermination tu as du voir que f(\fr{1}{3})=-frac{\sqrt{3}}{2} . Ainsi on peut transformer l'écriture et tombé sur : quelque chose de plus simple... \Large \fr{\sqrt(3&#...

A bon ?
(x-1) = -1 pour x=0
(1-x)= 1 pour x = 0
Donc pour ce qui est de l'égalité, on va avoir des problemes...

Comment continuerais-tu l'inégalité : (x-5) (1-x)<3(x²-1) ?

Qu'en penses-tu pour x=0 ?

Bonjour, Alors tout d'abord ta fonction est définie sur quel domaine ? \large \mathbb{R} ? \mathbb{R}^* ? etc Ensuite, il suffit d'écrire f(x)<0 si et seulement si (x-5) (1-x)-3(x²-1) < 0 si et seulement si (x-5) (1-x)<3(x²-1) ensuite tu continues pour te ramener à des choses ou on peut trouver le s...

Bonjour, Effectivement on peut exprimer les primitives de \large x \to e^{-\sqrt{(3x+2)}} . Déjà ta fonction est continue sur tout intervalle de R donc elle admet des primitives. Tu peux chercher une primitive à l'aide des définitions de ton cours ( \Bigint_{a}^{x} e^{-\sqrt{(3x+2)}}...

Bonjour, une solution simple quand on ne connait pas de primitive de ln(x) est d'utiliser les intégrations par partie : \large \Bigint_{a}^{b} ln(x-1)dx = [g(x)ln(x-1)]_{a}^{b} - \Bigint_{a}^{b} \fr{g(x)}{x-1}dx Ou g est une primitive de la fonction \large x \to 1 . I...

La dérivée 1ere est la somme de deux produits de fonction sur le meme model. \Large \fr{\partial^2 (f\circ \phi)}{\partial x^2} = \fr{\partial u}{\partial x}(x,y)( \fr{\partial^2 f}{\partial u^2}(u,v)\fr{\partial u}{\partial x}(x,y) + \fr{\partial^2 f}{\partial v ...

Salut Alors si je ne dis pas de betise on a : Si tu as ta fonction \large \\ f : \mathbb{R^2} \to R \\ (u,v) \to f(u,v) au moins C1 Et tu as la fonction \large \phi : \mathbb{R^2} \to \mathbb{R^2} \\ (x,y) \to (u,v) au moins C1, alors tu peux écrire que \Large \fr{\pa...