Forum de Mathématiques: Maths-Forum

pour et Df est la différentielle dans
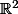
pour l'inégalité: oui pour tout , il existe une constante C qui dépend de epsilon
A montrer:

l'énoncé de l'exercice n'est pas vraiment lisible.
Essaye de l’écrire.

S.V.P pourriez vous me faire ce calcul, parce que je galère Soit f(z)=\frac{u}{\sqrt{1+|u|^2}}\big( e^{-1+\sqrt{1+|z|^2}}-1\big) Montrer que |Df(z)|\leq C_\varepsilon |z|^2(e^{\varepsilon|z|^2}-1) Je vous serai reconnaissant si vous me donner les détails du calcul.

Bonsoir, j'essayerai de te dépanner, ton problème est un classique de la fonction Gamma. pour la première question, il faut voir que pour tout 0\leq t\leq 1 et x réel positif tu distinguera les cas : 0\leq x\leq 1 et x\geq1 on a: 1\geq t^{x-1}\geq 0 n'oublions pas de dire que la fonction :t\mapsto t...

il n'y a personne qui peut m'aider S.V.P ?

Bonjour, Voici la fonction f(u)=\frac{u}{\sqrt{1+|u|^2}}(exp(-1+\sqrt{1+|u|^2})-\sqrt{1+|u|^2}) mon objectif est de trouver une telle majoration |df(u)-df(v)|\leq C_\varepsilon|u-v|\big(exp(\varepsilon |u|^2) -1+exp(\varepsilon |v|^2)-1\big...

je suis tout à fait d'accord avec toi, je suis aussi nul en calcul, je n'ai pas réussis à obtenir la majoration exacte en faisant deux fois différencier la fonction, j'ai employé le T.A.F et la convexité de l'exponentielle, je ne trouve qu’un seul (-1). i.e

Voici la fonction f(u)=\frac{u}{\sqrt{1+|u|^2}}(exp(-1+\sqrt{1+|u|^2})-\sqrt{1+|u|^2}) mon objectif est de trouver une telle majoration |df(u)-df(v)|\leq C_\varepsilon|u-v|\big(exp(\varepsilon |u|^2) -1+exp(\varepsilon |v|^2)-1\big) ave...

je crois qu'on peut utiliser le théorème des accroissements finis puis la convexité de l'exponentielle.

Merci pour votre réponse.
Maintenant, je veux la majorer de cette manière

avec C une constante qui dépend de epsilon.
Est -il possible?

je me suis trompé, en fait je cherche Df(u) sur de la fonction suivante :

Bonjour,

je voudrai connaitre la différentielle de cette fonction en 2 dimensions:

\frac{u}{\sqrt{1+|u|^2}}(exp(-1+\sqrt{1+|u|^2})-1)

raito123 a écrit:Tu peux donner tout l'énoncé car ces deux inégalité n'ont rien avoir avec le titre de la discussion?
Comme ça on verra claire ce qui est demander.

cé ca exactement l enoncé
c est une application sur le theoreme des acroissements finis ( inegalité)

raito123 a écrit:Tu peux donner tout l'énoncé car ces deux inégalité n'ont rien avoir avec le titre de la discussion?
Comme ça on verra claire ce qui est demander.

cé ca exactement l enoncé
c est une application sur le theoreme des acroissements finis ( inegalité)

Rain' a écrit:moi je trouve -8 et 4 et pas -4 et 4

cet exercice est absurde a ce ke je croit il y a certainement une faute sur le livre je suis mm certain

klevia a écrit:Je suis d'accord avec Rain',
je trouve -4 f'(x) 4

supposons ke cé correct comment deduire la 2)

Rain' a écrit:C'est vrai que le 2 est bizarre, t'es sur de ton énoncé ?

un casse tete!!!!!!!bof

Rain' a écrit:f ' ' est positive donc f ' est croissante donc comprise entre f(-1) et f(1)

dsl mais ca abouti a rien!!!!!!!!!!

on donne f(x)=x^4 +x^2 -2x +5
1) montrer que pour tout x de [-1,1] on a :-102) en deduire que pour tt x de ]-1,1[ on a: -10x +1merci de m aider!!!!!!!!
__________________