Forum de Mathématiques: Maths-Forum

Bonjour,

Ah oui désolé, j'ai confondu le max (1/2n) et le majorant proposé (M/n²).
Merci encore !

Bonjour, merci pour ta réponse

Oui, mais de ce fait, cette phrase (ci-dessous) est fausse non ?

, , .

En effet, cette majoration ne fonctionne pas quel que soit n dans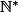 , il faut que n>M ?

Bonjour, je sèche sur cet exercice qui provient du Gourdon page 226. Soit u_n définie sur \mathbb R+ pour tout n \in \mathbb N^* par u_n(x)=\dfrac{x}{n^2+x^2} . Le but est de prouver que , pour M>0 , \sum u_n converge normalement sur [0;M] . Voici ce que je ne comprends pas: il est écrit que...

D'accord, merci beaucoup !

Bonjour, je lis souvent que si f est une fonction convexe sur un intervalle I et si a un élément appartenant à l'intérieur de I, alors f'_g(a) \le f'_d(a) . Il me semble sur le dessin que c'est nécessairement une égalité puisque les fonctions convexes sont continues... Est-ce...

Bonjour, merci pour votre réponse
Donc, si j'ai bien compris:
Si est diagonalisable, alors admet un polynôme annulateur P scindé à racines simples. Le polynôme minimal de divise P donc est nécessairement scindé à racines simples.

Bonjour, Je travaille avec le Gourdon (algèbre bien entendu !). Soit E un ev de dim finie. L'auteur a démontré le théorème des polynômes annulateurs: un endomorphisme f est diagonalisable si et seulement si il admet un polynôme annulateur scindé à racines simples. Plus tard, après avoir introduit la...

Très bien, merci beaucoup pour ton aide. Je viens à l'instant d'arriver au bout de la preuve, ouf !
Il ne me reste plus qu'à peaufiner certains détails (définition d'une vitesse de convergence quadratique, preuve du théorème de Taylor Lagrange...) mais je devrais m'en sortir seul.

Bonne journée

D'accord, merci ! Pourrait-on par exemple dire: puisque g' est continue sur un segment, alors elle est bornée et atteint ses bornes. Donc, le fait que sur le segment, |g'(x)|<1 et que sa borne sup, disons k, est atteinte, alors |g'(x)| \le k sur le segment avec k \in [0;1...

Bonjour à tous, Dans la suite de la preuve, je suis gêné par une affirmation. On a une fonction g définie sur un intervalle I_1 centré en \alpha (la solution de f(x)=0 ). Cette fonction g est dérivable de dérivée continue sur I_1 . Le but de la fin de la preuve est de prouver qu'il existe un...

Je tenterai de poster mes autres interrogations la semaine prochaine, je veux prendre le temps de bien les rédiger. Encore merci pour ton aide, ce n'est pas la première fois que tu me sort de l'embarras !

Tu as très certainement raison ! Effectivement, j'ai lu dans ce bouquin que l'on coupe en deux l'intervalle et qu'il faut être du bon côté. J'ai lu dans un autre, mais très rapidement, survolé serait le terme, que si on est du mauvais côté, on passe du bon côté au bout d'une étape. Après, il y a peu...

Bonjour et merci ! Je prendrai le temps demain matin d'étudier en détail la fonction que tu m'as proposé. Merci pour ton retour concernant les différents détails que j'ai donné. Depuis, j'ai encore une ou deux questions, faudra que je prenne le temps de les exposer ! Pour ce qui est des hypothèses, ...

Bonjour, je m'attaque à la démonstration de la méthode de Newton. Je m'appuie sur le Ketrane/Elineau qui propose une démonstration inspirée du Rombaldi, éléments d'analyse réelle. Ayant survolé la démonstration, je sens bien que ça va être un peu difficile pour moi. J'ouvre donc une discussion dans ...

D'accord, merci pour votre réponse, c'est très clair à présent ! Je vais essayer de tenir compte de vos conseils mais parfois, le temps manque hélas !
Bon weekend

Bonjour, Je n'arrive pas à me convaincre d'une démonstration. Soit (G , .) un groupe cyclique d'ordre n et a un générateur de G. Je souhaite donc prouver que si d divise n, il y a exactement \phi(d) éléments d'ordre d(indicatrice d'Euler). Je connais déjà le résultat suivant: l'ordre de a^{k...

Bonjour, merci pour votre réponse. Je pense avoir compris... Ker(f) et Ker(g) sont tous deux de dimension n-1. Donc, si l'un était inclus dans l'autre cela contredirait l'égalité des dimensions puisque un sous espace vectoriel F d'un espace vectoriel E qui a la même dimension que E est E tout entier.

Bonjour, Soient f et g deux formes linéaires non nulles sur un espace vectoriel de dimension finie. Je cherche à prouver qu'il existe un vecteur u de E tel que f(u) \neq 0 et g(u) \neq 0 . J'ai la correction mais n'arrive pas à en comprendre un passage. Si les formes linéaires sont p...

Oui oui, tout à fait, j'ai bien compris à l'aide de ton précédent message. Merci encore

Merci pour cette réponse détaillée.
Ce que je n'avais pas bien cerné, c'était plutôt avec la première définition. Car lorsqu'on dit, par définition, la forme linéaire telle que si i=j et 0 sinon, alors cette définition n'a de sens que si cette forme linéaire existe.