Forum de Mathématiques: Maths-Forum

Je réponds à ma propre question : On montre facilement que F est croissante. Si on suppose en plus que F est majorée alors \lim\limits_{x\to+\infty} F(x) = L\in\R^+ . Pour 0<x<y , on a alors : F(y)-F(x) = \int_x^y f(t) dt - yf(y)+xf(x) \geq \int_x^y f&...

Bonjour,

Soit de classe sur 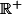, strictement décroissante et qui tend vers en .
On pose .
Comment montrer que si est majorée alors converge ?

Voici les idées qui me viennent : 1) \bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*) \subset(X\in n\N^*) , donc : P\left( (X\in n\N^*)\cap \overline{\bigcup\limits_{k=2}^{+\infty}(X\in kn\N^*)}\right) = P( X\in n\N^*) - P\left(\bigcup\limits_{k=2}^{+\i...

Bonjour GaBuZoMeu,
Merci pour ta réponse.
Oui, c'est à cause de cette égalité-là que je ne suis pas pleinement satisfait...
Je dirai : grâce à l'hypothèse "pour tout ", je vois bien que ce n'est pas très clair..

Bonjour, J'ai lu dans le sujet "Centrale Maths 2 PC 2018" que, si deux variables X et Y à valeurs dans \N^* vérifient : pour tout a\in\N^*,\; P(X\in a\N^*)=P(Y\in a\N^*) , alors X et Y suivent la même loi. Je voudrais démontrer cette affirmation et voici mon idée : (X=n...

Bonjour, En notant S_n = \sum\limits_{k=1}^{n}k^n , j'ai classiquement tenté une comparaison avec une intégrale, mais ça n'est pas assez précis, j'obtiens seulement qqch qui permet d'avoir l'intuition que S_n\sim C\times n^n avec C\in[1,2] . Quelques simulations numériques confirment que S_n\sim \fr...

Bonjour, Je réponds à ma propre question. En fait, je pense qu'ici on utilise la version plus générale du théorème sur les suites de fonctions continues qui convergent uniformément, à savoir (référence Gourdon Analyse) : Si (E,d) et (F,\delta) sont deux espaces métriques et (f_n&...

Merci encore, phyelec, pour votre réponse. Je suis surpris de ne pas trouver une définition claire et précise dans la littérature mathématique. On considérerait donc l'application de \R^n dans \R^n canoniquement associée à la matrice ? Pour information, et pour être un peu plus précis, ce dont je pa...

Bonjour phyelec et merci pour votre réponse. Je me suis sans doute mal exprimé. Je comprends bien les différentes notions de convergence (simple, uniforme, normale) pour des séries de fonctions, mais je ne suis tout simplement pas certain de la définition lorsqu'il s'agit d'une fonction de M_n(\...

Bonjour, En lisant une démonstration, je me suis posé une question. La démonstration consiste à montrer que l'exponentielle de matrice ( A\mapsto e^A=\sum\limits_{k=0}^{+\infty}\frac{A^k}{k!} ) est continue sur M_n(\R) . L'auteur fait cela sur un compact de M_n(\R) et montre la conve...

Bonjour et merci pour ta confirmation.
Je me demande si d'autres membres du forum ont un avis sur la question ?
L'introduction de ce segment [1,2] me semble totalement non justifiée et du coup je ne peux m'empêcher de penser que quelque chose m'a échappé...

Pas de réponse rapide. Cependant en cherchant un peu dans la littérature, j'ai vu qu'il y a une preuve du cas général dans "Oraux X - ENS, Algèbre Tome 1, p.331" : Si V est un sev de M_n(R) tel que toute matrice de V à un rang inférieur ou égal à p alors dim(V) <= np. Il doit être possible...

...montrer qu'il existe un vecteur non nul commun au noyau de toutes ces matrices... Bonjour, j'espère ne pas dire de grosses bêtises, mais es-tu sûr de ta démarche ? Parce que si je considère F le s.e.v. de M_3(\R) contenant toutes les matrices telles que la troisième ligne est la somme de...

Bonjour GaBuZoMeu,
Oui, effectivement, on a pas besoin de , Merci !
Pour revenir au post de adexvectorquantic, je ne suis toujours pas certain d'avoir vraiment compris sa question...

Bonjour,
Je ne suis pas sûr de comprendre ta question/remarque ?
Dans le lemme auquel tu fais référence, on a qui est injective avec 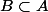et , donc fatalement la restriction de à est injective aussi...

Pour information, il s'agit du document suivant question 7.(d) : https://licence-math.univ-lyon1.fr/lib/exe/fetch.php?media=pmi:ds2_-_partie_ccp_autour_de_la_fonction_zeta_de_riemann_.pdf

Bonjour, Je suis en train de lire un corrigé sur le développement asymptotique de la fonction \zeta en 1^+ . L'auteur procède comme suit, avec x>1 : \zeta(x)-\frac{1}{x-1} = \zeta(x) - \int_{1}^{+\infty}\dfrac{dt}{t^x} = \sum\limits_{n=1}^{+\infty} \left(\frac{1}{n^x} - \int_{n}^...

Bonjour,
Merci à vous tous pour vos réponses ! La contraposée est très intéressante également, merci Ben314.

Bonjour, Après une bonne nuit de sommeil, voici ce que j'ai trouvé. Peut-être quelqu'un pourrait-il me dire si mon raisonnement lui semble correct (ou pas). Pour tout a\in A on note \delta_a = d(a ,\, A\backslash\{a\}) . Remarquons que \delta_a >0 car sinon a serait point d'accumulation. On ...

Edit : dans mon 2) je voulais bien sûr dire une injection de dans une partie de 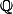et non pas le contraire comme je l'ai écrit...