53 résultats trouvés
Revenir à la recherche avancée
Re: Endomorphisme et matrices
D'accord merci beaucoup !
- 30 Aoû 2023, 07:21
- Forum: ✯✎ Supérieur
- Sujet: Endomorphisme et matrices
- Réponses: 6
- Vues: 393
Re: Endomorphisme et matrices
Oui donc ce serait alors plus la première option ?
- 29 Aoû 2023, 18:22
- Forum: ✯✎ Supérieur
- Sujet: Endomorphisme et matrices
- Réponses: 6
- Vues: 393
Re: Endomorphisme et matrices
Super merci beaucoup, j'ai envie de dire P(X)= Q(X-1) mais ça me semble beaucoup trop simple. Après je confonds peut-être les notations mais si on prends P(X)= 2X² +3, P(X+1) fait 2(X+1)² + 3 ou 2X² + 4?
- 29 Aoû 2023, 13:19
- Forum: ✯✎ Supérieur
- Sujet: Endomorphisme et matrices
- Réponses: 6
- Vues: 393
Re: Fonction qui s'annule sur [0;1]
Merci beaucoup, je pensais à une fonction '' à construire '' en disant par exemple que f vaut x entre moins l'infini et 0, 0 entre 0 et 1 et X entre 1 et plus l'infini mais cette fonction est-elle bien continue ?
- 29 Aoû 2023, 13:16
- Forum: ✯✎ Supérieur
- Sujet: Fonction qui s'annule sur [0;1]
- Réponses: 5
- Vues: 499
Endomorphisme et matrices
Soit n ≥ 1 entier et E = Rn[X], l'espace vectoriel des polynomes de degré inférieur à N. On considère l'application f : E -> E définie pour P appartenant à E par : f(P) = P(X+1). Je n'arrive pas a trouver la réponse à ces questions : Donner la matrice A de l'endomorphisme f dans la base β=(1,X,X²,X³...
- 29 Aoû 2023, 12:18
- Forum: ✯✎ Supérieur
- Sujet: Endomorphisme et matrices
- Réponses: 6
- Vues: 393
Fonction qui s'annule sur [0;1]
Bonjour,
Je cherche a trouver une fonction de R dans R, continue, non nulle mais qui s'annule sur l'intervalle [0;1] merci d'avance pour votre aide
Je cherche a trouver une fonction de R dans R, continue, non nulle mais qui s'annule sur l'intervalle [0;1] merci d'avance pour votre aide
- 29 Aoû 2023, 12:00
- Forum: ✯✎ Supérieur
- Sujet: Fonction qui s'annule sur [0;1]
- Réponses: 5
- Vues: 499
Re: Limite d'une application
GaBuZoMeu a écrit:J'attends toujours que tu explicites la notation.
C'est pour f restreinte a L
- 09 Jan 2023, 17:18
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une application
- Réponses: 14
- Vues: 704
Re: Limite d'une application
Oui mais justement, il faut qu'elle soit ni injective ni surjective de L dans L
- 08 Jan 2023, 16:21
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une application
- Réponses: 14
- Vues: 704
Re: Limite d'une application
Peut-être tan ?
- 08 Jan 2023, 15:13
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une application
- Réponses: 14
- Vues: 704
Re: Limite d'une application
Merci beaucoup, cependant, je ne comprends pas, ici,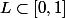 , mais sin est bien injective sur cet intervalle
, mais sin est bien injective sur cet intervalle
- 08 Jan 2023, 15:04
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une application
- Réponses: 14
- Vues: 704
Limite d'une application
On appelle limite d'une application f de E dans E l'ensemble L :
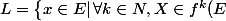\right\})
Je cherche un exemple d'ensemble E et d'application f de E dans E telle que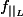 ne soit ni injective ni surjective et L non vide
ne soit ni injective ni surjective et L non vide
Je cherche un exemple d'ensemble E et d'application f de E dans E telle que
- 08 Jan 2023, 12:29
- Forum: ✯✎ Supérieur
- Sujet: Limite d'une application
- Réponses: 14
- Vues: 704
Re: Somme de binomiaux
Je trouve en réalité que cela correspond à la partie entière de (2^n)/r
Mais comment cela ce fait-il ?
Mais comment cela ce fait-il ?
- 27 Nov 2022, 15:04
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
Pour ce qui est de cette formule,
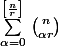
Je me demande ce qu'elle représente pour le triangle de Pascal, concrètement elle représente quoi ?
Je me demande ce qu'elle représente pour le triangle de Pascal, concrètement elle représente quoi ?
- 27 Nov 2022, 09:28
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
D'accord je vois merciiiii vraiment, c'est génial
- 27 Nov 2022, 09:26
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
Pour en déduire l'égalité suivante. \sum_{p=0}^{\left[n/4 \right]}{\begin{pmatrix} &n & \\ & 4p & \end{pmatrix}} = 2^{n-2} +2^{(n-2)/2}cos(\frac{n\pi }{4}) C'est la démonstration de cette formule qui pose problème ? Oui c'est ça m, vous la faite en utilisant les form...
- 26 Nov 2022, 18:46
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
\text{je suis en fait parti de } (1+i)^{n} \text{ et } (1-i)^{n} Que j'ai développé séparément à l'aide de la formule du binôme pour trouver deux expressions contenant chacune la somme dont je cherche le résultat. Par combinaison linéaire j'ai résolu ce système et ait trouvé la form...
- 26 Nov 2022, 16:56
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
, je n'arrive pas a déduire cette formule des deux précédentes: \sum_{p=0}^{\left[n/4 \right]}{\begin{pmatrix} &n & \\ & 4p & \end{pmatrix}} = 2^{n-2} +2^{(n-2)/2}cos(\frac{n\pi }{4}) i) Développer (1+i)^n avec la formule du binôme et l'égaliser à la forme tr...
- 26 Nov 2022, 16:49
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
Non j'ai q a la place de α, mais q étant l'indice de ma somme aussi, c'est pareil
- 26 Nov 2022, 16:38
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
après calculs, je trouve: \Large \dfrac{1}{r} \sum_{k=0}^{r-1} \, (1+\omega_{r}^k)^n=\sum_{\alpha=0}^{\left[\frac{n}{r} \right]} \, \binom{n}{\alpha r } Il n'y aurait pas une erreur d'énoncé ? Si c'est exact c'était bien cela, excepté que a la place de α j'ai r mais cela ne change rien du t...
- 26 Nov 2022, 15:53
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
Re: Somme de binomiaux
Wahou merci c'est vraiment impressionnant je vois pas comment j'aurais pu trouver ça tout seul ...
- 26 Nov 2022, 15:49
- Forum: ✯✎ Supérieur
- Sujet: Somme de binomiaux
- Réponses: 25
- Vues: 941
- 53 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
