Forum de Mathématiques: Maths-Forum

Merci pour vos réponses et votre aide. je pense maintenant avoir compris.

Donc on peut conclure qu'effectivement 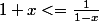, c'est bien cela ?

Expliqué comme cela c'est effectivement plus clair et beaucoup plus compréhensible. Alors étant donné que \frac{x^{2}}{x - 1} est négatif et que 1 + x - \frac{1}{1 - x} = \frac{x^{2}}{x - 1} on peut en déduire que 1 + x - \frac{1}{1 - x} est négatif aussi. Mais négatif ne veut pas dire = 0, donc 1 +...

Encore une fois merci beaucoup pour vos réponses. C'est terrible parce que j'ai beau relire les précédents messages, je ne comprends toujours pas pourquoi lorsqu'on demande : peut-on conclure que 1 + x <= \frac{1}{1 - x} il faut chercher le signe de \frac{x^{2}}{x - 1} pour avoir la réponse :( Je me...

Merci pour votre réponse. J'ai pris cet exemple de x = 0.5 parce que ce nombre (0.5) est > 0 et < 1 : il est dans l'encadrement. C'était juste pour illustrer. Il suffit de soustraire chaque membre par -1 dans l'inégalité x < 1 pour obtenir x - 1 < 0 , soit : x - 1 < 1 - 1 x - 1 < 0 J'ai du mal à voi...

Oups j'ai oublié en cours de route que je dois étudier le signe de l'expression pour 0 <= x < 1 donc x ne peut pas être > à 1 et x ne peut pas être < à 0 non plus. Donc x est > 0 et inférieur à 1. Si je prend comme exemple x = 0.5 alors 0.5 - 1 = -0.5 (donc résultat négatif), donc x - 1 est négatif....

Mon cours s'arrête au signe d'un produit, signe d'un quotient et il dit : Règle des signes: Soit a et b deux réels différents de 0. - si a et b ont le même signe, alors a x b et \frac{a}{b} sont positifs. - si a et b sont de signes contraires, alors a x b et \frac{a}{b} sont négatifs. Donc pour étud...

Mon cours s'arrête au signe d'un produit, signe d'un quotient et il dit : Règle des signes: Soit a et b deux réels différents de 0. - si a et b ont le même signe, alors a x b et \frac{a}{b} sont positifs. - si a et b sont de signes contraires, alors a x b et \frac{a}{b} sont négatifs. Donc pour étud...

Je te suggère de te servir de l'égalité précédente en étudiant le signe de \frac{x^2}{x-1} Vous parlez de cette égalité 1 + x - \frac{1}{1 - x} ? Comment j'étudie le signe de \frac{x^2}{x - 1} Je pense avoir la solution : on peut conclure que si x >= 0 et x < 1 alors 1 + x <= \frac{1}{1 - x} , est-...

Merci pour vos réponses. Et est-ce qu'on peut dire que \frac{-a}{-b} = -\frac{a}{b} ? Alors maintenant qu'on a pu justifier que 1 + x - \frac{1}{1 - x} = \frac{x^{2}}{x - 1} il y a le b) : b) Peut-on conclure que 1 + x <= \frac{1}{1 - x} ? Alors on a une inégalité qui est sous la forme A <= B et on ...

Merci, je comprends mieux maintenant. Comment arrivez-vous à simplifier si rapidement de \frac{1 - x^2 - 1}{1 - x} = \frac{x^{2}}{x - 1} ? Il n'est pas nécessaire de montrer tout le chemin de simplification pour arriver à \frac{x^{2}}{x - 1} ? Est-ce que cette simplification est juste : \frac{1 - x^...

Comme cela ? 1 + x - \frac{1}{1 - x} = \frac{1 - x}{1 - x} + \frac{x(1 - x)}{1 - x} - \frac{1}{1 - x} = \frac{1 - x}{1 - x} + \frac{x - x^2}{1 - x} - \frac{1}{1 - x} = \frac{1 - x + x - x^2 - 1}{1 - x} = \frac{-x^2}{1 - x} = \frac{-1(-x^2)}{-1(1 - x)} = \frac{x^2}{-1 + x} = \...

Encore merci pour vos explications (qui m'aident beaucoup). Donc si je vous ai bien compris, je pars de 1 + x - \frac{1}{1 - x} et je cherche à trouver \frac{x^{2}}{x - 1} . Donc : 1 + x - \frac{1}{1 - x} \frac{1(1-x)}{1 - x} + \frac{x(1-x)}{1 - x} - \frac{1}{1 - x} \frac{1(1-x&#...

Merci pour vos réponses.

Autant je vois ce qu'il faut faire pour résoudre une équation mais je ne vois pas ce qu'il faut faire pour "Montrer que pour tout x, A(x)=0" : je ne sais comment formuler cela par écrit et je ne sais par ou commencer pour (dé)montrer cela

Merci pour votre réponse. Eh ben j'ai encore du boulot :( L'énoncé vous donne très précisément la réponse à la question "x est-il différent de 1", vérifiez-le. Oui x est différent de 1 puisque dans 0 <= x < 1 le x est strictement inférieur à 1. Ou alors c'est de dire "montrons que pou...

Bonjour à tous, J'ai l'exercice ci-dessous à faire à la maison : X désigne un nombre réel tel que 0 \leq x < 1 a) Justifier que 1 + x - \frac{1}{1 - x} = \frac{x^{2}}{x - 1} b) Peut-on conclure que 1 + x \leq \frac{1}{1 - x} J'aurais besoin qu'on me dise si mon raisonnement et mes calculs ci-dessous...

Merci pour toutes vos réponse et votre aide.

Merci pour votre réponse. En effet il me manquait la façon de rédiger, quand je vous lit ("pour tout x réel, si x est compris entre 0 et 1 alors x² est inférieur à x") tout est clair et 100% compréhensible :) Une question tout de même : pourquoi on part du x<=1 comme hypothèse et non pas d...

Comment expliquer maintenant que x^2<=x ? On peut déduire de l'inégalité 0<=x<=1 que x >= 0 (donc x est positif) et que x est >=0 et x <=1. Si l'on remplace par exemple dans x^2<=x le x par 1 on obtient 1x1<=1 soit 1<=1 ce qui est correct comme résultat. Si l'on remplace le x par 0 on obtient 0x0<=0...

Merci pour votre réponse. Grâce à vos explications, j'ai compris la chose suivante dans : si a < b et si c > 0, alors ac < bc et a/c < b/c , est-ce équivalent de dire : si a < b et si c est positif , alors ac < bc et a/c < b/c ? Si j'ai x < 10 et si je multiplie le tout par 3 (chiffre positif), j'ob...