Forum de Mathématiques: Maths-Forum

bonsior

il y a beaucoup de solutions

par exemple 3007 divisé par 55 =54 reste 37

non tu a tu te tromper .tu tois trouver x=??

commence par dévelloper (x-2)2 puis passe les terme avecles x de l'autre côté

oui ça doit être ça

:++: :++: :++: :++: pour tous tes conseils :we: :we: :we: :we: :happy2: :happy2: :happy2: :happy2:
a plus

oui d'acord ça fait 1-1/µ

est que l'on peu dire que -1/µ = -µ+1

car on a démontré précédemment u-1=1/µ



donc on remplace 1-1/µ = 1-µ+1 = 2-µ

oui je trouve bien 1/µ^2 mais je n'arrive pas a trouver 2-µ en faisant u-1/u

oui je trouve bien 1/*^2 sauf que je n'arrive pas a trouver 2-µ

Je sais je suis lourd :mur:

donc il faut faire µ-1/µ =


et (1/µ)/µ = 1/µ*1/µ = 1/µ^2

je trouve donc µ-1-1/µ=0
µ-1=1/µ


puis il faut déduire que 1/u^2=2-µ

donc ça donne µ-1-1/µ=0

µ-1=1/µ

donc:

puis on divise tout par


je vois pas ce que tu veux dire :help:

donc:

puis on divise tout par [/quote]


je vois pas ce que tu veux dire :help:

donc:

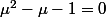
puis on divise tout par et le travail est quasiment fini[/quote]


je vois pas ce que tu veux dire :help:

:triste: aucune idée

je me suis trompé dans l'énoncé c'est x^2-x-1 donc en fait µ=1+racine5/2
la question 2 est bonne

oui c'est vrai le nombre d'or est -1+racine5/2

:marteau:

mais pas d'erreur pour la question 2 il faut démontrer que 1-µ=1/µ
puis en déduire que 1/µ^2=2-µ

quelqun a une idée pour la question 2

Le nombre d'or est la solution positive de l' équation x²+x-1=0 donc ici
il n'y a q'une solution

oui tu a raison delta=5 donc µ= 1+racine5/2

Bonjour, mon DM est à rendre pour la rentrée des vacances Le nombre d'or est la solution positive, noté µ de l'équation (e): x^2+x-1 1. Déterminer la valeur de µ 2. montrer que µ-1=1/µ en déduire que 1/µ^2=2-µ Remarque question 1 et 2 sont indépendantes Je bloque sur la question 2 . pour la une je p...