7 résultats trouvés
Revenir à la recherche avancée
Re: intégrale
Bonjour Rdvn, tout d'abord je m'excuse pour la réponse tardive. Vous avez bien raison, il y avait un faute de frappe dont ma prof ne s'est pas rendu compte, et moi non plus. il s'agit de (\frac{-1}{3})^{n+1} au niveau de la première question. de plus je suis encore en lycée, c'est juste que ...
intégrale
bonsoir, voici un problème que je n'arrive pas à résoudre: 3) soit n \in \mathbb{N} \space , S_n =\sum_{k=0}^{n}(\frac{-1}{3})^k \frac{1}{2k+1} et R_n =\int_{0}^{1}t^{2n+2}f(t)dt a. montrer que f(t)=\sum_{k=0}^{n}(-1)^k(\frac{1}{\sqrt{3}})^{2k}+(\frac{-1}{...
Re: suite définie par intégrale
merci énormément!
- 03 Fév 2021, 17:10
- Forum: ✎✎ Lycée
- Sujet: suite définie par intégrale
- Réponses: 2
- Vues: 256
suite définie par intégrale
bonjour, quelqu'un pourrait m'aider?
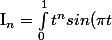dt) . trouver une relation entre
. trouver une relation entre 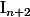 et
et 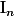 .
.
j'ai pensé à faire une intégration par parties mais je ne sais pas comment commencer.
j'ai pensé à faire une intégration par parties mais je ne sais pas comment commencer.
- 03 Fév 2021, 15:53
- Forum: ✎✎ Lycée
- Sujet: suite définie par intégrale
- Réponses: 2
- Vues: 256
Re: Maths question
bonjour/bonsoir, 1. la vitesse en nœuds et la valeur de 1 nœud en km/h étant données, tu peux calculer la vitesse du Nautilauï en km/h. puis rappelle-toi de la relation v = d/t 2. (je ferais de mon mieux ici) il faut vérifier si le nombre de cases rouges est la moitié du nombre total de cases (50% d...
- 04 Jan 2021, 23:06
- Forum: ✎ Collège et Primaire
- Sujet: Maths question
- Réponses: 2
- Vues: 412
Re: nombre complexe
merci énormément!
- 28 Déc 2020, 16:09
- Forum: ✎✎ Lycée
- Sujet: nombre complexe
- Réponses: 3
- Vues: 264
nombre complexe
bonjour, voici mon problème: soient x, y et z des nombres complexes de module 1. prouver que \lvert{xy + xz + yz}\rvert = \lvert{x+ z + y}\rvert j'ai pensé à cette égalité: x\bar{x}=y\bar{y}=z\bar{z} afin d'écrire x, y et z en fonction de \bar{x} , \bar{y} et \bar{z} puis factoriser et je sais plus ...
- 28 Déc 2020, 15:24
- Forum: ✎✎ Lycée
- Sujet: nombre complexe
- Réponses: 3
- Vues: 264
- 7 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
