17 résultats trouvés
Revenir à la recherche avancée
Re: Calcul d'intégrale
Pour la seconde tu intègres par partie, sinon pour la première ca devient plus complexe..
- 12 Déc 2020, 17:58
- Forum: ✯✎ Supérieur
- Sujet: Calcul d'intégrale
- Réponses: 6
- Vues: 309
Re: Fonction implicite
Si si mais je n'ai jamais rencontré ce cas, ça me paraissait bizarre, je pensais m'être trompé dans mes calculs.
D'accord super je vous remercie pour vos réponses.
D'accord super je vous remercie pour vos réponses.
- 10 Déc 2020, 11:27
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Re: Fonction implicite
J'obtiens juste donc comme =(0,0)~et~que~\frac{\partial{\varphi}}{\partial{y}}=1~donc~j'ai~au~final~ y=0) mais ca me parait bizarre de trouver 0.
mais ca me parait bizarre de trouver 0.
Je ne sais pas si j'ai encore une équations de droite après.
Je ne sais pas si j'ai encore une équations de droite après.
- 10 Déc 2020, 09:14
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Re: Fonction implicite
Bah si mais la déjà le fait que ca soit plusieurs variable me perturbe et de plus je ne vois pas ce qu'on fait enfaite avec les fonctions implicites. Comme mon prof ne donne pas de cours de maths a distance c'est compliqué de comprendre toutes les notions. Sinon j'aurais fait (x-x_0)\frac{\p...
- 09 Déc 2020, 08:55
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Re: Fonction implicite
Alors enfaite je ne vois pas comment trouver l'équation de la droite tangente. Je sais que je peux faire : \frac{\partial{\psi(0)}}{\partial{x}}=-\frac{\frac{\partial{\varphi(0,0)}}{\partial{x}}}{\frac{\partial{\varphi(0,0)}}{\partial{y}}} et en remplaçant je trouve \frac{\pa...
- 08 Déc 2020, 20:40
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Re: Fonction implicite
Bonjour, oui je sais bien, j'aurais dû mettre plus d'élément dans la question. Ce que j'ai fais en plus de l'énonce, est: Tout d'abord j'ai regardé ce que me donnais la fonction au voisinage de l'origine, on a: \varphi(x=0,y=0)=0 Ensuite j'ai donc calculé les dérivées partielles de la foncti...
- 08 Déc 2020, 09:37
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Fonction implicite
Bonjour, je suis bloqué sur un exo, en réalité je ne comprend pas la démarche pour ce type d'exo. Je vous le cite: Soit~la~fonction~\varphi~des~deux~variables~x~et~y~suivante: \\~\varphi:\mathbb{R}\times\mathbb{R}\longrightarrow\mathbb{R}/(x,y)\longrightarrow\varphi(x,y)=x^2cos(y...
- 07 Déc 2020, 18:46
- Forum: ✯✎ Supérieur
- Sujet: Fonction implicite
- Réponses: 10
- Vues: 370
Re: Equations aux dérivées partielles
Super j'en prend note, merci beaucoup pour votre aide.
Passez une excellente journée
Passez une excellente journée
- 24 Nov 2020, 11:17
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Re: Equations aux dérivées partielles
Oui effectivement ca doit marcher à coup sur, et vous trouvez le même résultat donc ?
- 24 Nov 2020, 11:13
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Re: Equations aux dérivées partielles
ok d'accord merci et cela conclue donc l'exo. Oui j'ai vérifié et toute fonction ) et c'est bon.
et c'est bon.
Je voulais vous demandez si la démarche est bonne ?
Je voulais vous demandez si la démarche est bonne ?
- 24 Nov 2020, 09:14
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Re: Equations aux dérivées partielles
Bonsoir, si je comprend bien il faut que g(x;y)=F(x),~~\forall F et donc que f(u(x;y);v(x;y))=F(\sqrt{uv}),~~\forall F . Ceci serait la condition nécessaire mais je ne vois pas ce que peut être la condition suffisante. Sinon était-il judicieux de remar...
- 23 Nov 2020, 22:57
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Re: Equations aux dérivées partielles
Comme  on en déduis donc que
on en déduis donc que =C^{cst}) mais cette constante peut potentiellement dépendre de x.
mais cette constante peut potentiellement dépendre de x.
Après je ne suis pas sur. Mais je ne trouve pas d'autre façon de conclure le problème.
Après je ne suis pas sur. Mais je ne trouve pas d'autre façon de conclure le problème.
- 23 Nov 2020, 18:10
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Equations aux dérivées partielles
Bonjour, à toutes et a tous. Je cherche à résoudre un exercice ou l'on me demande de chercher les solutions d'une EDP. Je vous cite l'exo en question : On~veut~resoudre~dans~\mathbb{R_{+}^{*}}\times\mathbb{R_{+}^{*}}~l'EDP suivantes : \\u\frac{\partial{f}}{\partial{u}}-v\frac{\partial{f}}{\parti...
- 23 Nov 2020, 03:04
- Forum: ✯✎ Supérieur
- Sujet: Equations aux dérivées partielles
- Réponses: 11
- Vues: 479
Re: Fonction a pls variable
Bonjour oui excusez moi il y a un - entre y et z dans la racine merci beaucoup pour vos réponse j'avais réussi a trouver par moi même par contre j'avais noté la racine ) pour simplifier mon calcul.
pour simplifier mon calcul.
Merci.
Merci.
- 21 Nov 2020, 10:14
- Forum: ✯✎ Supérieur
- Sujet: Fonction a pls variable
- Réponses: 4
- Vues: 297
Re: Changement de variable
Pour ) il faut utiliser les dérivations composer en posant
il faut utiliser les dérivations composer en posant )=arctan(g))
Ensuite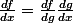
avec=e^x) et donc
et donc )=arctan(g))
après tu remplace g par sa valeurs
Ensuite
avec
après tu remplace g par sa valeurs
- 16 Nov 2020, 20:08
- Forum: ✯✎ Supérieur
- Sujet: Changement de variable
- Réponses: 12
- Vues: 696
Re: Changement de variable
Essaie en posant : u=x+1, u'=1 et dx=(1/u')du
Puis calcul d'abord l'intégrale sans borne.
Puis calcul d'abord l'intégrale sans borne.
- 16 Nov 2020, 18:47
- Forum: ✯✎ Supérieur
- Sujet: Changement de variable
- Réponses: 12
- Vues: 696
Fonction a pls variable
Bonjour a toutes et a tous. Je bloque sur un des exercices de ma feuille de TD de maths, normalement le fichier avec l'énoncé de l'exercice est disponible ci dessous. S'il n'est pas lisible ou ouvrable je copie l'énoncé ici : Soit l'équation : z^2 + (2/x) = \sqrt{y^2 + z^2} Montrer que l'équ...
- 16 Nov 2020, 14:42
- Forum: ✯✎ Supérieur
- Sujet: Fonction a pls variable
- Réponses: 4
- Vues: 297
- 17 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
