21 résultats trouvés
Revenir à la recherche avancée
Re: Résultat different avec le taux liés
Effectivement, après reboot de la calculatrice j'ai le bon résultat
- 23 Fév 2021, 20:57
- Forum: ✎✎ Lycée
- Sujet: Résultat different avec le taux liés
- Réponses: 2
- Vues: 368
Résultat different avec le taux liés
Bonjour, Je viens de voir que j'ai 2 résultats différents sur un même problème et je ne vois pas d'où vient la faute. Le problème est le suivant. J'ai un robinet qui avec un débit de 1.2m^3/h et je veux remplir une piscine de r=3,66m et une hauteur de 1,4m. Combien de temps vais-je mettre En passant...
- 23 Fév 2021, 19:27
- Forum: ✎✎ Lycée
- Sujet: Résultat different avec le taux liés
- Réponses: 2
- Vues: 368
Re: Domaine d'une limite dans une racine
Spyrakos, pourrais-tu faire un petit effort pour lire et comprendre ce qu'on te dit ? On te serine sur tous les tons que si Ce n'est pas de la mauvaise volonté. Je comprends que quelque chose m'échappe dans votre raisonnement et je cherche simplement des exemples pour mieux visualiser votre façon d...
- 22 Fév 2021, 10:36
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Re: Domaine d'une limite dans une racine
Pourquoi on aurait pas pu dire \ge 0) ?
?
Ce qui me dérange le plus c'est l'exclusion du 0, car est définie
est définie
Ce qui me dérange le plus c'est l'exclusion du 0, car
- 22 Fév 2021, 09:50
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Re: Domaine d'une limite dans une racine
Une des réponse que je vois c'est que 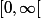 est un intervalle et sur un intervalle, la continuité d'une limite est définie si elle est continue dans l'intervalle
est un intervalle et sur un intervalle, la continuité d'une limite est définie si elle est continue dans l'intervalle 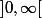 et que
et que =f(a))
- 22 Fév 2021, 09:08
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Re: Domaine d'une limite dans une racine
Merci de l'attention portée à l'aide que je t'ai fournie. Je n'ai pas encore compris le message que tu as voulu me dire. Je suis d'accord que l'on peut avoir f(x)<0 et \lim_{x\to a}=0 . Mais je ne vois pas en quoi cela justifie que \lim_{x\to a}f(x)>0 s'il est dans une racine pair a...
- 22 Fév 2021, 08:26
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Re: Domaine d'une limite dans une racine
fibonacci a écrit:bonsoir
exact n dit être de la forme 2k.
Merci pour ton aide très pertinente à me question
- 21 Fév 2021, 19:41
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Domaine d'une limite dans une racine
Bonjour,
Je vois que}=\sqrt[n]{ \lim_{x\to a} f(x)}) mais il faut que
mais il faut que >0) pour
pour  pair. Ce que je ne comprends pas c'est pourquoi cela doit être plus grand que 0. Le domaine d'une racine c'est
pair. Ce que je ne comprends pas c'est pourquoi cela doit être plus grand que 0. Le domaine d'une racine c'est 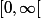 et non
et non 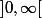
Je vois que
- 21 Fév 2021, 11:42
- Forum: ✯✎ Supérieur
- Sujet: Domaine d'une limite dans une racine
- Réponses: 14
- Vues: 676
Difference entre évaluer une limite et une fonction
Bonjour, J'ai du mal à voir la difference entre évaluer une fonction et une limite. Je m'explique soit f(x)=\frac{4-2x}{3x+1} si j'évalue \lim\limiter_{x\to3}f(x) c'est exactement la même chose que f(3) . Si je suis dans le cas d'une forme indéterminé comme f(x)=\frac...
- 19 Fév 2021, 14:21
- Forum: ✯✎ Supérieur
- Sujet: Difference entre évaluer une limite et une fonction
- Réponses: 1
- Vues: 291
Déterminer la méthode de factorisation pour les limites
Bonjour Possible que je me trompe mais évaluons \lim\limits_{x\to 1} \frac{x^3+x^2-5x+3}{x^3-3x+2} Si je pars sur une double factorisation j'ai \lim\limits_{x\to 1} \frac{(x-1)(x^2+2x-3)}{(x-1)(x^2+x-2)}=...=\lim\limits_{x\to1}\frac{x+3}{x+2}=\frac 4 3 Mais si je pars...
- 18 Fév 2021, 23:34
- Forum: ✯✎ Supérieur
- Sujet: Déterminer la méthode de factorisation pour les limites
- Réponses: 3
- Vues: 417
Difference entre cosec et sin^-1
Bonjour,
Si je ne me trompe pas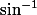 est la fonction inverse de
est la fonction inverse de 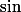 càd
càd 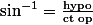 . Mais quelle est la difference entre
. Mais quelle est la difference entre 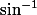 et
et  . J'ai l'impression que c'est pareil
. J'ai l'impression que c'est pareil
Si je ne me trompe pas
- 14 Fév 2021, 08:49
- Forum: ✎✎ Lycée
- Sujet: Difference entre cosec et sin^-1
- Réponses: 3
- Vues: 340
Réciprocité d'une fonction exponentielle si a < 0
Bonjour, Je vois que la fonction log_b x est la réciprocité de fonction exponentielle b^x . Mais la fonction exponentielle est défini dans x \in \R alors que la fonction log_b x \in \R^+ . Là ou je bug c'est quand a < 0. Il y a bien une fonction réciproque. Par exemple g(x)=-2(3^x) a...
- 13 Fév 2021, 12:47
- Forum: ✎✎ Lycée
- Sujet: Réciprocité d'une fonction exponentielle si a < 0
- Réponses: 1
- Vues: 182
Re: Comment choisir la façon de factorisé un trinôme
Merci pour la réponse Euh non, c'est plutôt (attention au signe et il faut aussi remplacer le coefficient constant) Sur le livre que je lis (mise à niveau mathématique de josée hamel) c'est ce qu'il y a pourtant https://i.ibb.co/c3wGJqp/Screenshot-2021-02-04-at-11-51-46.png Et dans le cas de x^2+bx+...
- 04 Fév 2021, 11:56
- Forum: ✎✎ Lycée
- Sujet: Comment choisir la façon de factorisé un trinôme
- Réponses: 3
- Vues: 326
Comment choisir la façon de factorisé un trinôme
Bonjour, Je vois que je peux factorisé un trimôme de la forme ax^2+bx+c avec deux méthodes 1. avec le discriminant Delta 2. L'écrivant sous la forme ax^2+mx+nx+c \ \text{tel que} \ m,n \in\Z et mn=ac et m+n=b Ce que je ne comprends pas bien, c'est dans quel cas on privilégie l'une ou l'autre. Elle m...
- 04 Fév 2021, 11:29
- Forum: ✎✎ Lycée
- Sujet: Comment choisir la façon de factorisé un trinôme
- Réponses: 3
- Vues: 326
Re: Factorisation d'une difference de cerrée
Merci. Effectivement je comprends mieux.
Que voulez-vous dire pas on sait "plus facilement" traiter du signe ?
Que voulez-vous dire pas on sait "plus facilement" traiter du signe ?
- 03 Fév 2021, 20:40
- Forum: ✎✎ Lycée
- Sujet: Factorisation d'une difference de cerrée
- Réponses: 4
- Vues: 249
Factorisation d'une difference de cerrée
Bonsoir, J'ai une info qui m'échappe. a^2-b^2=(a-b)(a+b) Pourquoi si j'ai 36-121x^2=-(11x-6)(11x+6) j'ai un - qui est comprehensible, mais ce n'est plus de la forme (a-b)(a+b) c'est -(b-a)(b+a) avec a qui change de signe et non b
- 03 Fév 2021, 20:24
- Forum: ✎✎ Lycée
- Sujet: Factorisation d'une difference de cerrée
- Réponses: 4
- Vues: 249
Re: Mise au même dénominateur d'une inéquation
Le passage sur chaque ligne c'est bon je l'ai compris 
L'histoire qu'il voit 5x/6 indépendamment du 3/4 me perturbe un peut, car je ne vois pas pourquoi il a choisi de faire ça
L'histoire qu'il voit 5x/6 indépendamment du 3/4 me perturbe un peut, car je ne vois pas pourquoi il a choisi de faire ça
- 11 Nov 2020, 16:27
- Forum: ✎✎ Lycée
- Sujet: Mise au même dénominateur d'une inéquation
- Réponses: 4
- Vues: 564
Mise au même dénominateur d'une inéquation
Bonjour, Sur un livre j'ai ceci comme exemple https://i.ibb.co/k03nMCP/Screenshot-2020-11-11-at-15-06-38.png Sauf que pour moi, mettre au même dénominateur \frac{5x}{6}-\frac{3}{4} c'est de la forme \frac{a}{b}-\frac{c}{d}=\frac{ad-cb}{bd} et non voir indépendamment \frac{5x}{6} et \frac{3}{4} pour ...
- 11 Nov 2020, 15:28
- Forum: ✎✎ Lycée
- Sujet: Mise au même dénominateur d'une inéquation
- Réponses: 4
- Vues: 564
Re: Factorisation d'un trinôme
J'ai du mal à suivre.
m+n=10 et -b/a=-25/16 donc m+n != -b/a. Pareil pour mn = 9 et c/a = 9/16
m+n=10 et -b/a=-25/16 donc m+n != -b/a. Pareil pour mn = 9 et c/a = 9/16
- 10 Nov 2020, 19:19
- Forum: ✯✎ Supérieur
- Sujet: Factorisation d'un trinôme
- Réponses: 4
- Vues: 302
Factorisation d'un trinôme
Bonjour, Je fais des exos sur les factorisations et je me pose une question. Soit 16x^{2}+25x+9 j'obtiens une factorisation de (16x+9)(x+1) avec le théorème P=a(x-r_{1})(x-r_{2}) et utilisant b^{2}-4ac . Mais je vois aussi que la factorisation d'un trinôme de la forme...
- 10 Nov 2020, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Factorisation d'un trinôme
- Réponses: 4
- Vues: 302
- 21 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
