Forum de Mathématiques: Maths-Forum

Merci de votre réponse , je viens de comprendre

Bonjour , je ne comprends pas comment faire pour la question 2 et 3 , Pour la 2 j'ai posé l'équation (|z+1|/|z-1| = 1) , j'arrive donc à |z+1|=|z-1| , mais je ne vois pas comment conclure. Pour la 3 j'ai fais de même en posant (|z+1|/|z-1| = racine(2) ) , mais cela ne me mène à rien Merci de votre r...

Ah oui pardon , On considère un espace vectoriel E de dimension 3 muni d’une base U = (u1, u2, u3) et un endomorphisme f de E ayant pour matrice dans la base U : \begin{pmatrix} 0& 1 & 0\\ 1& 1 &1 \\ 0&1 &0 \end{pmatrix} 1) Calculer A^2 et A^3 2)Montrer par récurrence que pou...

Bonjour , je n'arrive pas a faire cet exercice , si quelqu'un pourrait me donner des pistes ça serait gentil , merci et bon weekend. Montrer par récurrence que pour tout entier n strictement positif on a : \begin{pmatrix} a_{n} & a_{n+1} & a_{n}\\ a_{n+1} & a_{n+2} & a_{n+1}\\ a_{n} ...

Bonjour , c'est un exercice de physique mais c'est la partie mathématiques que je n'ai pas compris : Je ne comprend pas comment mon prof passe de : 2*y*exp(j(wt-pi/2)) à 2y*cos(wt-pi/2) Je ne comprend pas pourquoi ce n'est pas : 2y*cos((wt-pi/2)+j*sin(wt-pi/2)) Est ce que c'est parce que il ne peut ...

Bonjour J'ai été absent pas mal de temps et j'ai un exercice de proba à faire j'aurais besoin de piste , merci de votre aide : Selon l’administration fiscale américaine (IRS), en 2019, une déclaration des revenus sur cent est contrôlée lorsque le revenu du contribuable est inférieur à un million de ...

Bonjour J'ai été absent pas mal de temps et j'ai un exercice de proba à faire j'aurais besoin d'aide : 1. Combien de numéros de téléphone fixe peut-on attribuer en France métropolitaine sachant que : • l’indicatif de région est 01, 02, 03, 04 ou 05, • les deux chiffres suivants sont distincts • de n...

Merci beaucoup pour l'aide je vais faire ça

Bonjour , j'ai besoin d'aide pour un exercice , je ne sais pas comment l'aborder:

Soit f une fonction continue sur [0;1] à valeur dans [0;1]. En considérant la fonction : g(x)= f(x)-x , montrer qu'il existe un réel a appartient à [0;1] tel que : f(a) = a

Merci de votre aide

Merci beaucoup je vais essayer dans la soirée

Bonsoir ,
Je bloque sur un exercice :

Soit (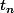) une suite telle que pour 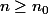on a :



avec a>0. Montrer que : pour 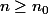puis que (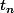) est divergente.

Merci de votre aide

Oui effectivement pardon , c'était

Bonsoir ,
Je bloque sur un exercice :

Soit (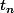) une suite telle que pour 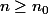on a :



avec a>0. Montrer que : pour 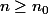puis que (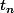) est divergente.

Merci de votre aide

A oui , merci beaucoup

Tu supposes que pour un certain entier n 0 \leq u_n \leq \dfrac{1}{n+1} Sur cet intervalle, f est croissante donc 0 \leq u_{n+1} \leq f\left( \dfrac{1}{n+1} \right) Il suffit de montrer que f\left( \dfrac{1}{n+1} \right) \leq \dfrac{1}{n+2} Bonsoir et merci , Je ne trouve pas f croi...

Bonjour ,
Oui j'ai pensé a faire une récurrence mais je ne vois pas comment m'y prendre
L'initialisation est bonne mais pour l'hérédité je ne vois pas comment faire

Bonjour , je bloque dans mon DM de maths : Soit f la fonction définie sur R par f(x) = -x² + x et (Un) la suite défini par : Uo ∈ ]0,1[ ∀n >= 0 , Un+1 = f(Un) 1) Etudier les variation de f (On trouve f(x) croissant de -infini à -1/2 et décroissant jusqu'a -infini) 2) Mq pour tout n ∈ N , 0<Un< 1/(n+...