Forum de Mathématiques: Maths-Forum

Où sont tes résultats ?

sdsdsdfsqsd

Bonjour, Voici le topo, je bloque sur une question, car il me manque un truc: (O;\vec{u};\vec{v}) est un repère orthonormal direct du plan complexe. On considère le point A d'affixe z_A=1+i On note S_1 la symétrie orthogonal direct par rapport à l'axe (O;\vec{u}) et h l'homothétie de...

On me demande une équation de P_1 plan médiateur à [AB] . A(4;0;-3) B(2;2;2) \vec{AB} (-2;2;5) \vec{AB} est un vecteur normal à P_1 . Donc -2x+2y+5z+d=0 est une équation de P_1 . M milieu de [AB] , d'où M(3;1;\frac{-1}{2}) (je ne suis pas sur du tout que ce soit les b...

Savez-vous calculer l'équation d'un plan médiateur d'un segment, en ayant les coordonnées des points de ce segment ?

Personne ne peut m'aider, s'il vous plait, je sais que je parais impatient, mais c'est pour faire la suite du DM. ;)

Bonjour, J'ai un DM, et je n'arrive pas à faire une démonstration. Sphère circonscrite à un tétraèdre. [AB] est un segment et M est son milieu. 1.a.Démontrer que si N appartient au plan médiateur à [AB] alors NA = NB. C'est une évidence, mais je ne sais pas comment le prouver. :s J'ai pensé à un pre...

Bonjour, J'ai une égalité à démontrer, et je suis arrivé à la fin, et j'ai un doute, enfin je vous explique. Montrer que pgcd(a;b)=pgcd(bc-a;b) avec a , b et c entier naturels non nuls. Voici ce que j'ai fais: pgcd(a;b)=d pgcd(bc-a;b)=d' d|a et d|b d'où d|bc et d|...

J'avais fais une erreur de calcul à la question 3, donc ça me bloquait ici ^^. Le DM est terminé, merci à vous. ;)

Je trouve toujours pas, mais bon, 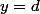, donc 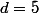ou .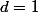

Question suivante:

En déduire le , de et en fonction de .

Là j'dois avouer que j'arrive à rien. :doh: :dodo:

Pour cette question, c'est réglé, la suivante aussi. a = n^3+2n^2-3n b = 2n^2-n-1 Il fallait montrer que a et b sont divisibles par (n-1) a = (n-1)(n^2+3n-6) b = (n-1)(2n+1) Le problème est donc réglé. Ensuite, on a d PGCD de n(n+3) et (2n+1) ...

leon1789 a écrit:heu pourquoi ?

Donc

Donc (ou ?).

leon1789 a écrit:oui, et cela conduit-il à des conclusions intéressantes ?

Intéressantes ? Je n'sais pas.

Mais pour le cas

On a .
Ce qui est plutôt différent de .

J'ai fais comme ceci (j'avais pas pensé):


et
d'où
d'où
Donc .

.

Edit: Le soucis, c'est qu'on mettre d'autres coefficients.

Genre 3\alpha-\beta, etc....

D'accord merci. J'voulais être sur, car sur la question suivante, je bloque. On pose \alpha = n+3 et \beta = 2n+1 et on note \gamma le PGCD de \alpha a et \beta . a.Calculer 2\alpha-\beta et en déduire les valeurs possibles de \gamma . 2\alpha-\beta=5 Que dois-je en déduire ? Car \gamma=pgcd(\al...

Bonjour. n est un entier naturel supérieur ou égal à 2. 1.Montrer que n et 2n+1 sont premiers entre eux. On cherche donc à montrer que pgcd(n;2n+1)=1 J'ai débuté comme ceci: On a d, tel que pgcd(n;2n+1)=d. D'où d|n. D'où d|2n. On a d|2n+1, donc (par soustraction) d|1 Donc d=1 (car d est un pgcd, et ...

Je pensais que c'était sur R, forcément je comprends mieux.

J'vais le finir, merci à vous.

Initialisation n=0 f(x)=e^x-x A l'aide de la dérivée, et d'un tableau, on obtient f(x)>1 donc f(x)>0 pour tout x . Hérédité: Je suppose: f_{n}(x)>0 Je veux démontrer que: f_{n+1}(x)>0 f_{n}(x)>0 e^x-\frac{x^{n+1}}{(n+1)!}>0 f_{n+1}(x)>0...

D'où

Et c'est sur , donc si et , sur , ça va donner ?

Comment passer de

à ?

J'ai essayé avec un peu de calcul, à chaque fois, j'obtiens supérieur à un nombre avec des x et des k, et pas 0.

Par récurrence, en fonction de n et n+1 ?